Deriving Law of Cosines from Law of Sines

Question

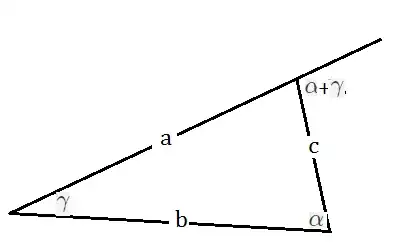
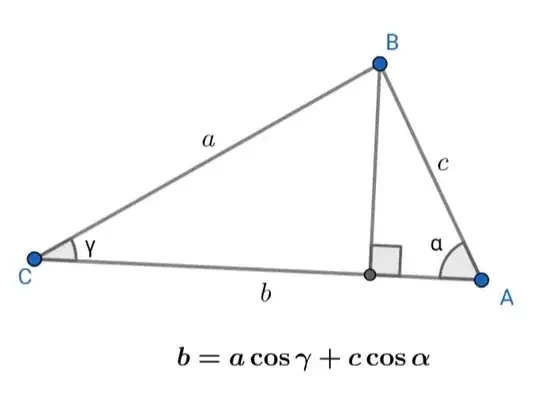
How to eliminate $\alpha$ from the Law of Sines of plane trigonometry

$$ \dfrac{a}{\sin \alpha}= \dfrac{c}{\sin \gamma} =\dfrac{b}{\sin (\gamma+\alpha)} =2R $$

in order to arrive at the Law of Cosines

$$ c^2= a^2+b^2-2 a b \cos \gamma \;?$$

Starting to isolate $\alpha$

$$ \alpha =\sin^{-1}\big(\dfrac{b-c}{2R} +\sin \gamma \big)-\gamma$$

$$ =\sin^{-1}( b \sin \gamma/c) -\gamma$$

involve $c$ that we are finding and so on, how best to simplify?

score 3 · Answer 1 · answered Dec 25 '21 at 14:07

3

First, let's get the following relationship.

From $$\frac{a}{\sin\alpha}=\frac{c}{\sin\gamma}=\frac{b}{\sin(\alpha+\gamma)}$$

using componendo and dividendo,

$$\frac{a\cos\gamma+c\cos\alpha}{\sin\alpha\cos\gamma+\cos\alpha\sin\gamma}=\frac{b}{\sin(\alpha+\gamma)}$$

$$a\cos\gamma+c\cos\alpha=b$$

However, these are unnecessary stuff since obviously,

Now, let's go back to our problem: deriving law of cosines from law of sines.

From law of sines we have, $$a\sin\gamma=c\sin\alpha$$ Squaring, $$a^2\sin^2\gamma=c^2\sin^2\alpha$$ $$a^2(1-\cos^2\gamma)=c^2(1-\cos^2\alpha)$$ $$a^2=c^2+a^2\cos^2\gamma-c^2\cos^2\alpha$$ $$a^2=c^2+(a\cos\gamma+c\cos\alpha)(a\cos\gamma-c\cos\alpha)$$ $$a^2=c^2+b\cdot(a\cos\gamma-c\cos\alpha)$$ $$a^2=c^2+b\cdot[(b-c\cos\alpha)-c\cos\alpha]$$ $$a^2=b^2+c^2-2bc\cos\alpha$$

$\blacksquare$

answered Dec 25 '21 at 14:07

ACB

3,713

@Narasimham , sorry I forgot that you are trying to eliminate $\alpha$. I have eliminated $\gamma$ here. But I hope you can do the same for $\alpha$. – ACB Dec 25 '21 at 14:09
1

Yes. Thanks for remembering for so long ! – Narasimham Dec 25 '21 at 14:18
1

+1. However, it's worth noting that, once you have established $b=a\cos\gamma+c\cos\alpha$, then you effectively already have derived the Law of Cosines: The companion relations, $c=b\cos\alpha+a\cos\beta$ and $a=b\cos\gamma+c\cos\beta$ make for a linear system in $\cos\alpha$, $\cos\beta$, $\cos\gamma$. Solving gives, for instance, $\cos\alpha=\frac{-a^2+b^2+c^2}{2bc}$. There's no reason to "go back" to the problem; you've solved it. :) – Blue Dec 25 '21 at 17:32

score 0 · Answer 2 · answered Jun 13 '20 at 18:37

0

Note that $a=2R\sin\alpha,\quad b=2R\sin\beta$ and $c=2R\sin\gamma.$ Now sbstitute these into the expression $$\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{(a+b+c)(a+b-c)}{2ab}-1$$ and simplify (until you get $\cos\gamma$ :)).

answered Jun 13 '20 at 18:37

Bumblebee

18,220
5
47
87

@Narasimham: Are you asking for a step by step simplification? I am not asking any question here, but answering to your original question. – Bumblebee Jun 13 '20 at 18:47
Yes, the trig/algebra simplification steps.. – Narasimham Jun 13 '20 at 18:55

score 0 · Answer 3 · answered Jun 13 '20 at 19:17

0

Hint

$$a^2+b^2-c^2$$

$$=4R^2(\sin^2A+\sin^2B-\sin^2C)$$

Use Prove $ \sin(A+B)\sin(A-B)=\sin^2A-\sin^2B $

and $$\sin(B+C)=\cdots=\sin A $$

answered Jun 13 '20 at 19:17

lab bhattacharjee

274,582

score 0 · Accepted Answer · edited Dec 25 '21 at 15:48

$$\frac {b}{\sin(\gamma + \alpha)}= 2R.$$ $$\frac {b}{\sin(\gamma) \;\cos(\alpha)+ \sin\alpha \; \cos\gamma} = 2R.$$ From Law of Sines: $\sin\alpha = \frac {a}{2R} \;\; and\;\; \sin(\gamma)= \frac {c}{2R}.$

Then $$\frac {b}{\frac{c}{2R} \;\cos\alpha+ \frac{a}{2R} \; \cos\gamma} = 2R,$$ $$b= c\;\cos\alpha + a\;\cos\gamma,$$ $$b= c\;\sqrt{1-\sin^2\alpha} + a\;\cos\gamma.$$

From Law of Sines: $\sin\alpha = \frac{a\;\sin\gamma}{c}.$

Then $$b= c\;\sqrt{1-\frac{a^2\;\sin^2\gamma}{c^2}} + a\;\cos\gamma \;=\; \sqrt{c^2-a^2\;\sin^2\gamma} + a\;\cos\gamma$$ $$(b-a\;\cos\gamma)^2 = c^2-a^2\;\sin^2\gamma,$$ $$b^2+a^2\cos^2\gamma - 2ab\;\cos\gamma = c^2-a^2\;\sin^2\gamma,$$ $$b^2+a^2\cos^2\gamma - 2ab\;\cos\gamma + a^2\;\sin^2\gamma = c^2,$$ $$b^2+a^2(\cos^2\gamma + \sin^2\gamma) - 2ab\;\cos\gamma = c^2.$$

Since $\cos^2\gamma + \sin^2\gamma =1,$ $$b^2+a^2 - 2ab\;\cos\gamma = c^2.$$

Deriving Law of Cosines from Law of Sines

4 Answers4