3

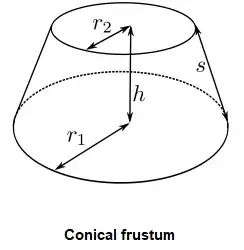
I will be starting my question with an argument on surface area of a frustum.

enter image description here

Let center of smaller face (with radius $r_2$) be placed on the origin of $x$-$y$ coordinate system.

Then, $y = f(x) = mx +$ $r_2$, will be equal the radius function with respect to $x$. For approximation of surface area we can Partition the interval $[0,h]$ into n sub-intervals.

$P = \{x_0, x_1, ...., x_n\}$ where, $x_0$= $0$ and $x_n$ = $h$.

Now, Lower approximation ($L$) for surface area can be done as:

$$L = \sum_{k=1}^n 2\pi f(x_{k-1})\Delta x_k $$

and for Upper approximation ($U$):

$$U = \sum_{k=1}^n 2\pi f(x_{k})\Delta x_k $$

But, $ \lim \limits_{||P|| \to 0} $ (U) = $ \lim \limits_{||P|| \to 0} $ (L) = $\int_0^h 2 \pi f(x) \,dx$

Solving this integral will result in:

Surface Area $= \pi h (r_1 + r_2)$, which is not correct.

Can anyone tell me, what am I doing wrong?? Then I will be posting my question further for the generalized definition of surface area (based on frustums).

Harish Chandra Rajpoot
  • 37,450
Harwinder Singh
  • 83
  • 1
    This is already discussed in one of my answers. But it uses the formula for frustum of cone as a basis. The surface area of frustum needs to be evaluated by some other means like cutting it to form a portion of a ring. – Paramanand Singh Jun 13 '20 at 09:16
  • @ParamanandSingh Thanks for the comment. While i was reading your answer on the mentioned post, i was still thinking like this, "If a quantity can be overestimated and underestimated by a Riemann sum, then it should always be trapped inside the two and the limit should give the value of the quantity." Can you tell your views on that? Because i think the Riemann sum formed by cylindrical slices overestimate and underestimate the value of surface area (even for a generalized function). – Harwinder Singh Jun 13 '20 at 13:34
  • 1
    Well your Riemann sums in question only underestimate and never overestimate. – Paramanand Singh Jun 13 '20 at 13:38
  • 1
    Moreover just like arc-length the surface area of a curved surface can only be approximated from below. The case of arc-length is easy to understand (because of 2D) and is given in this answer. – Paramanand Singh Jun 13 '20 at 13:53
  • @ParamanandSingh I just realized that it does not overestimate, but not always, only when slope is very large. Strange!!! – Harwinder Singh Jun 13 '20 at 13:54
  • Wow!! I just found out by trials that as slice gets smaller and smaller every cylinder starts underestimating for a common slope. But to prove it in general should be tough i think. But it answers my question, – Harwinder Singh Jun 13 '20 at 14:17
  • 1
    Note that volume of a frustum lies between the volume of cylinders based on smaller and larger radii, but the same idea can not be extended to surface area of the curved part of frustum. It is quite possible to be misguided in this manner. But after some experiments one can convince that this is a false belief. – Paramanand Singh Jun 13 '20 at 14:21
  • Yes, you are right. If it is proved rigorously, then we can say that Riemann sum given by cylinders cannot be used to determine surface area (because it does not give the surface area of frustum properly). But even after that it requires proof that Riemann sum given by frustums does compute the surface area in the limit. Or can we just define surface area like that (a thing computed by sum of frustums)? – Harwinder Singh Jun 13 '20 at 14:38
  • 1
    Well the analysis of the surface area is far more complicated and it is best to accept that the Riemann sums corresponding to area of a frustum slices indeed give the surface area of the surface of revolution. – Paramanand Singh Jun 13 '20 at 14:49
  • okay, it is acceptable. – Harwinder Singh Jun 13 '20 at 14:53

2 Answers2

2

This is a classic mistake. You're replacing the area of a frustum with the area of a cylinder, even in the tiny pieces. The height is not the same as the slant height. (There's a reason that the correct calculus formula uses the arclength of the curve, not the vertical height.)

Ted Shifrin
  • 115,160
  • I can understand what you say. But, i asked the question for this same reason. If a quantity can be overestimated and underestimated by a Riemann sum, then it should always be trapped inside the two and the limit should give the value of the quantity. Is it not? – Harwinder Singh Jun 13 '20 at 06:12
  • 2
    @HarwinderSingh The actual surface area is not bounded above by the upper estimate. If the slant height is large (a long sloping cone), you can see this quite easily. – Ted Shifrin Jun 13 '20 at 06:27
  • Thanks for the comment and answer. It does underestimate for every case I think. – Harwinder Singh Jun 13 '20 at 14:42
1

You should consider the slant length $dl$ which is given as $$dl=\sqrt{1+\left(\frac{dy}{dx}\right)^2} dx=\sqrt{1+\left(\frac{d}{dx}(mx+r_2)\right)^2} dx=\sqrt{1+m^2}\ dx$$

The surface area of differential element of frustum of thickness $dx$ is $2\pi y\ dl$. Integrating ths area with proper limits, the surface area $A$ of frustum of cone is by obtained as follows $$A=\int_0^{h}2\pi y\ dl=\int_0^{h}2\pi (mx+r_2)\sqrt{1+m^2}dx$$ Where $m=\frac{r_1-r_2}{h}$

Harish Chandra Rajpoot
  • 37,450