-1

Using differential equations , I have seen some sites which solve the fibonacci number problem and give us a formula to find the nth fibonacci number.

Similarly I want to find the nth fibonacci number where each number is equal to "LAST THREE" numbers.

Example :

0 1 1 2 4 7 13 .....

How to get the exact formula to find the Nth fibonacci number by removing the recursion from it ?

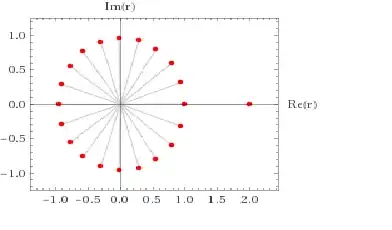
F(n) = F(n-1) + F(n-2) + F(n-3)

After solving the differential equations :

F(n) = Expression of constants which only depends on "n" .

What is the formula for F(n) ?

Also is it possible to get a formula to find the Nth fibonacci number where each number is equal to the sum of previous "M" numbers ? 

F(n,m) = ???

Note : I am not a math student :/

Natesh bhat
  • 141
  • What have you tried? – David G. Stork Jun 12 '20 at 06:50
  • This is called the Tribonacci sequence (I find that an amusing pun), and it's discussed here: https://math.stackexchange.com/questions/827565/how-to-find-the-nth-term-of-tribonacci-series – Matti P. Jun 12 '20 at 06:53
  • i have updated my question – Natesh bhat Jun 12 '20 at 06:53
  • If the characteristic polynomial of the recurrence only has simple roots in $\mathbb{C}$ the main term has the form $$A_n = \sum_{k=1}^{d} C_k \zeta_k^n $$ where $\zeta_k$ ranges over the roots and $C_1,\ldots,C_d$ are constants depending on the initial values. This applies to the Fibonacci, Tribonacci, Tetranacci sequences etcetera. – Jack D'Aurizio Jun 12 '20 at 07:08
  • An interesting side-question is to find efficient algorithms for the computation of $F_n, T_n$ or $Q_n$. As shown here the computation of $F_n$ requires at most $2\log_2(n)$ multiplications. – Jack D'Aurizio Jun 12 '20 at 07:10

1 Answers1

1

The solutions of these generalized Fibonacci problems rest on the resolution of the characteristic equation

$$r^m=r^{m-1}+r^{m-2}+\cdots r+1.$$ which can also be written $$r^{m+1}-2r^{m}+1=0$$ or $$1-2s+s^{m+1}=0$$ (where the solution $r=1$ must be discarded, and $s:=r^{-1}$). This equation has real as well as complex roots. Hence the solution of the recurrence is a linear combination of terms $$(a\cos(n\omega)+b\sin(n\omega))e^{n\tau}$$ where the constants $a,b$ are determined from the initial terms of the sequence (which you forgot to specify) and $\tau,\omega$ are the real and imaginary parts of the roots.

Note that one of the roots clearly dominates the others in modulus, and tends to $2$ with increasing $m$. Hence for large $m$ and large $n$, the solution is close to

$$c2^n.$$

This is justified by

$$2^{m}\approx 2^{m-1}+2^{m-2}+\cdots 2+1.$$

enter image description here