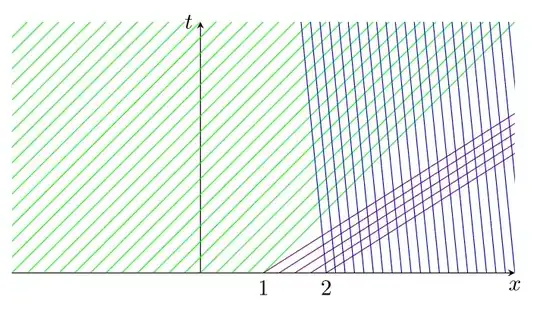
I'm trying to understand the actual solution which is computed here (Sec. 4.7 of Ref. (1)), trying to resolve $$ \begin{cases} \displaystyle \frac{\partial u}{\partial \tau} + \frac{\partial q}{\partial x} = 0, \\ u(0,x) = \frac{c_0}{c_{max}} = \begin{cases} 0, \quad \text{if} \quad x \le 0\\ u_0, \quad \text{if} \quad x \in ]0,1[ \\ 1, \quad \text{if} \quad x \ge 1 \end{cases}\\ u(\tau, 0) = 0\\ u(\tau ,h) = 1, \forall\tau > 0 \end{cases} $$ where $q(u) = u(1-u)(1-\beta u)$ with $\frac{1}{2} < \beta < 1$. First, he's trying to connect $0$ to $u_0$ with a shock wave: $$x(\tau) = \sigma(0,u_0)(\tau) = \dfrac{q(u_0)}{u_0}\tau$$ so the solution becomes $ u(t,x) = 0$ if $x <\sigma(0,u_0)\tau$, $u(t,x) = u_0$ if $1 > x >\sigma(0,u_0)\tau$, and $u(t,x) = 1$ if $x \ge 1$. Then he's trying to connect $u_0$ to $1$ by introducing an intermediate state which is $u_1$. How does it change the exact solution? He's only showing the final stationary state at the end.
the characteristics:
\begin{center}
\begin{tikzpicture}
\draw[-stealth] (-4,0)--(4,0) node[below]{$x$};
\draw[-stealth] (-1,0)--(-1,4) node[left]{$t$};
\node[below] at (0,0) {$1$};
\node[below] at (1,0) {$2$};
\clip (-4,0) rectangle (4,4);
\foreach \xi in {-8,-7.75,...,0} \draw[green] (\xi,0) -- (\xi+4,4);
\foreach \xi in {0,0.25,...,1} \draw[violet] (\xi,0) -- (\xi+4*1.575,4);
\foreach \xi in {1,1.15,...,5} \draw[blue] (\xi,0) -- (\xi-4*0.1,4);
\end{tikzpicture}
\end{center}
(1) S Salsa: Partial Differential Equations in Action: From Modelling to Theory, 3rd Ed. Springer, 2016. doi:10.1007/978-3-319-31238-5