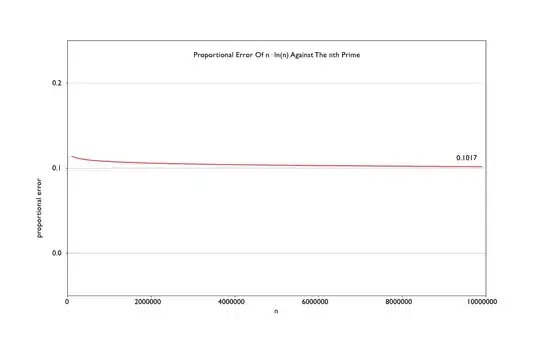
The following graph shows the proportional error of $n\ln(n)$ for the $n^{th}$ prime.
The proportional error appears to fall towards $0.1$, and not zero, when considering the first $n=10,000,000$ natural numbers.
- Is this a correct conclusion, or is this a case of a very very slow asymptotic approach to zero?
- Where can I find a proof of the non-zero limit?
In comparison, plots of the proportional error of $\frac{n}{ln(n)}$ and $\text{Li}(n)$ for the number of primes up to $n$, $\pi(n)$, do show it approaching zero more clearly.