I am following the book "Introduction to probability" from Bertsekas.
In the book the derivation of the mean of Geometric random variable is through the use of the Total expecation theorem which involves conditional expectation.
My problem is when I try to derive $E[X]$ I end up getting $E[X] = E[X]$ instead of $E[X] = \frac{1}{p}$
I am going to try to derive the mean. Please highlight where I may be wrong. I am still new to probability so please highlight any small mistakes as well.
$E[X] = \sum_{k=1}^\infty ( P(k) \times E[X | k]) = P(k = 1) \times E[X | k = 1] + P(k > 1) \times E[X | k > 1]$
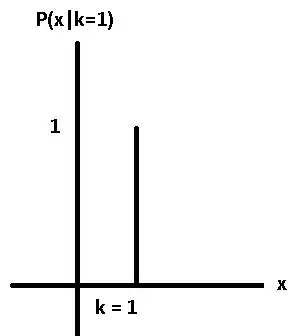
$P(k = 1) = p$
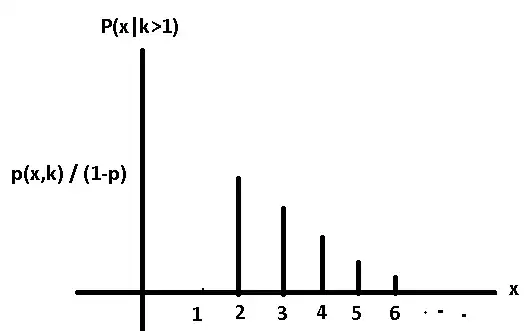
$P(k > 1) = 1 - p$ using sum of infinite geometric series formula
$E[X | k = 1] = 1 \times P(X | k = 1) = \frac{P(X \cap k = 1)}{P(k = 1)} = \frac{p}{p} = 1 $
The trouble is when I try to find $E[X | k > 1]$
$E[X | k > 1] = \sum_{k=2}^\infty ( k \times (P[X | k > 1]) $
$E[X | k > 1] = \sum_{k=2}^\infty ( k \times \frac{P(X \cap k > 1)}{P(k > 1)})$
$E[X | k > 1] = \sum_{k=2}^\infty ( k \times \frac{P(X \cap k > 1)}{(1-p)})$
$P(X \cap k > 1) = \sum_{k=2}^\infty ((1-p)^{k-1} \times p)$
I suspect the problem to be in the following line
$E[X | k > 1] = \frac{1}{(1-p)}\sum_{k=2}^\infty ( k \times \sum_{k=2}^\infty ((1-p)^{k-1} \times p)$
$E[X] = \sum_{k=1}^\infty ( k \times (1-p)^{k-1} \times p $
$E[X] = p + \sum_{k=2}^\infty ( k \times (1-p)^{k-1} \times p $
$\sum_{k=2}^\infty ( k \times (1-p)^{k-1} \times p = E[X] - p $
$E[X | k > 1] = \frac{E[X] - p}{1 - p}$
finally using the total expectation theorem
$E[X] = P(k = 1) \times E[X | k = 1] + P(k > 1) \times E[X | k > 1]$
$E[X] = p \times 1 + (1 - p) \times \frac{E[X] - p}{1 - p}$
$E[X] = E[X]$ ?? what is the meaning of this?
Thanks.