1

I am interested if there is geometric meaning (using graphs) of $(1 + \frac{1}{n})^n$ when $n \rightarrow \infty$. Also, is there visual explanation of why is $e^x = (1 + \frac{x}{n})^n$ when $n \rightarrow \infty$ and why is $\frac{d}{dx}e^x = e^x$?

I see that this kind of question is not posted yet.

Martin Sleziak
  • 53,687
1b3b
  • 1,276

2 Answers2

1

Exponentiation turns addition to product, $$a^{b+c}=a^ba^c$$ (in the naturals, this is immediate from the definition). This corresponds to a "translation" property: shifting the argument amounts to a multiplication by a constant, and conversely, multiplying by a constant preserves the shape.

By definition, the slope of a curve is the vertical increment corresponding to an horizontal increment, and by the above property, the vertical increment must be a constant times the function. Hence the derivative of an exponential is an exponential.

More specifically,

$$\lim_{h\to0}\frac{a^{x+h}-a^x}h=a^x\lim_{x\to h}\frac{a^h-1}h$$ confirms this intuition.

Now we have this "magical" number $$\lim_{x\to h}\frac{a^h-1}h,$$ which is a priori a function of $a$. When $a=1$, this is $0$; when $a=10$ (say), numerical estimates based on $h=2^{-k}$ are $9, 4.32\cdots,3.11\cdots,2.67\cdots,2.48\cdots,\cdots2.3025\cdots$. They seem to stabilize above $1$.

It is possible (I will not attempt here) to show that the limit indeed converges to a value above $1$ for $a=10$, and that it is a continuous function of $a$. Hence, by the IVT, the must exist a constant, let $e$, such that

$$\lim_{h\to0}\frac{e^h-1}h=1$$

and

$$(e^x)'=e^x.$$

The plot below illustrates the relation between an exponential and its derivative, by showing

$$3^x,3^{x+1}-3^x,3^{x+1}.$$

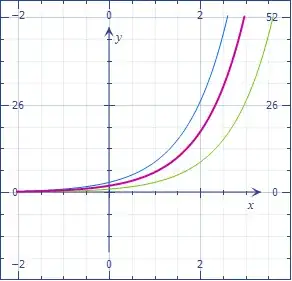
enter image description here

One can also show that

$$e^x=\lim_{n\to\infty}\left(1+\frac xn\right)^n$$ is truly a power function and

$$e^x=\left(\lim_{m\to\infty}\left(1+\frac1m\right)^m\right)^x$$ (it suffices to substitute $mx$ for $n$), and the definition of the natural exponential just rests on the constant $e$.

  • Thanks, but I asked for intuitive explanation of why are concepts of "selfderivation" and compound interest $((1 + \frac{1}{n})^n)$ when $n \rightarrow \infty$, we can see, equal. And again, thank you (this trick with $mx$ is very elegant). How can one logically conclude that this must be the case, that number which we get from compund interest is the base of nicely continuosly growing exponential function – 1b3b Aug 19 '20 at 21:42
  • 1
    @1b3b: I did answer for the "selfderivation" question, with a geometric interpretation. I don't understand the second part of your comment. The "nice continuity" does not follow from the particular value of the base. –  Aug 19 '20 at 21:53
  • "Nicely continuously growing" I meant that velocity of output change, $\frac{\Delta y}{\Delta x}$, is for $e^x$ exactly equal to the output (slope of a tangent line in point $(x_0, e^{x_0})$ is equal to $e^{x_0}$). In other words, derivative of $e^x$ is $e^x$. So, only $e^x \approx 2.71828^x$ have this property. Also, that same number $e$ is what we get in coumpund interest formula - why and how are this two concepts connected? I would be very thankful if you provide me some intuition for this :) – 1b3b Aug 19 '20 at 22:45
  • @1b3b: I guess that you did not understand my answer. There must be a number with that property and we call it $e$. –  Aug 20 '20 at 06:56
  • 1
    Sorry, maybe my question wasn't clear enough. I am interested in opposite direction (from limit to derivative property, not from derivative property to limit). So, how can one conclude that this number (which we get from compund interest!) $\lim_{n \to \infty} (1 + \frac{1}{n})^n$ is the base for $a^x$ when $(a^x)' = a^x$ intuitively? Is there a intuitive explanation or just algebra? – 1b3b Aug 20 '20 at 16:04
  • @1b3b: $$\frac{a^h-1}h\to 1, (h+1)^{1/h}\to a$$ –  Aug 21 '20 at 07:04
0

I think of my favorite, and pretty geometric, proof of this limit, using the squeeze or sandwich theorem for limits. You can do it using an upper and lower Riemann sum with one subdivision for the integral of $1/t$.

One has $L\le\int_1^{1+x/n}1/t\rm dt\le U\implies x/n(1/(1+x/n))\le\ln(1+x/n)\le x/n(1)\implies x/(n+x)\le\ln(1+x/n)\le x/n\implies e^{x/(n+x)}\le(1+x/n)\le e^{x/n}\implies e^{nx/(n+x)}\le(l+x/n)^n\le e^x$, and take limits.