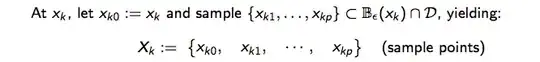Given a real rectangular matrix $X$, I would like to uniformly sample from the set of real rectangular matrices $\mathbb{M}$ that satisfy $||X-S||\leq \epsilon, \forall S\in\mathbb{M}$ and for a fixed real, scalar radius $\epsilon$.
Now procedurally/algorithmically, how can I obtain a matrix $\hat{S}$ (sample) by such a 'uniform sampling' within the specified radius? The key is that the sampling should be uniform when obtaining an instance $\hat{S}$. What would be the necessary steps to be taken to be able to do this?
The fact that the set $\mathbb{M}$ seems very large is why the notion of sampling really confuses me to be able to assign a probability law although the $\epsilon$ does constraint the set to an extent.
The following is what I am trying to do, i.e get a sample of the type $X_k$ as shown in the screenshots attached below: