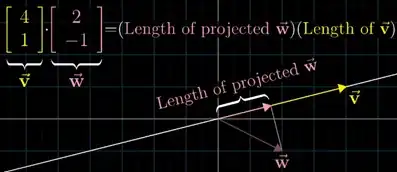
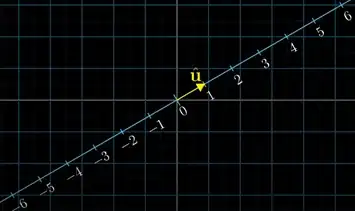
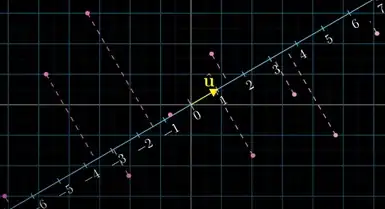
I am trying to understand visual interpretation of dot product from 3b1b series video. Here, he defines dot product as follows:
Dot product of $\vec{v}$ and $\vec{w}$ is multiplication of projection of $\vec{w}$ on $\vec{v}$ and length of $\vec{v}$.
Here, he gives explanation of how dot product is related to projections.
Here is what I can make out of it:
- Taking dot product of two vectors to get single number is similar to applying matrix transformation: $$\begin{bmatrix} a \\ b \end{bmatrix} . \begin{bmatrix} c \\ d \end{bmatrix} = \begin{bmatrix} a & b \end{bmatrix} . \begin{bmatrix} c \\ d \end{bmatrix} =a.b+c.d $$
- Given two vectors $\vec{u}$ and $\vec{v}$, lets plot a number line passing through the $\vec{u}$. Lets assume $\vec{u}$ is a unit vector denoted by $\hat{u}$?
- Defining projection transformation Projection transformation on this number line can be defined as follows:
Above each pink dot represent end point of a vector.- So, this projection transformation defines projection of any vector $\vec{v}$ on $\hat{u}$
- Such transformation is completely defined by projection of $\hat{i}$ and $\hat{j}$ on $\hat{u}$, where $\hat{i}$ and $\hat{j}$ are unit vectors on $x$ axis and $y$ axis respectively, that is $\hat{i}=\begin{bmatrix} 1 \\ 0 \end{bmatrix} $ and $\hat{j}=\begin{bmatrix} 0 \\ 1 \end{bmatrix} $. $\hat{i}$ will land at $u_x$ ($x$ coordinate of $\hat{u}$) and $\hat{j}$ will land at $u_y$ ($y$ coordinate of $\hat{u}$).
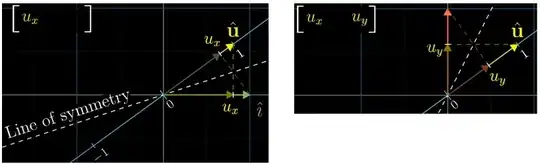
- Thus, this projection transformation is same as multiplying unit vector $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ by $\begin{bmatrix} u_x & u_y \end{bmatrix}$: $$\begin{bmatrix} u_x & u_y \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} $$ and according to point 1, this is same as dot product: $$\begin{bmatrix} u_x \\ u_y \end{bmatrix} . \begin{bmatrix} 1 \\ 1 \end{bmatrix} $$
(The video author further explains how this can be extended for non unit vector $\vec{u}$, but that is not the concern for my doubt.)
So, in above, I am able translate projection transformation to matrix multiplication and then to matrix dot product. But this is able to translate "projection transformation" (defined in point 3 and 4 above), which I guess, is not exactly "the multiplication of projection of $\vec{w}$ on $\vec{v}$ and length of $\vec{v}$ " as stated in first quote. Or is it, but I am not able perceive? If yes, what I am missing? If no, how we can translate "multiplication of projection of $\vec{w}$ on $\vec{v}$ and length of $\vec{v}$ " to dot product of $\vec{v}$ and $\vec{w}$?