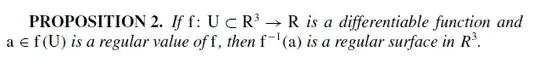1

Given this definition:

enter image description here

and the following theorem:

enter image description here

This theorem does not mention anything about whether $f$ is injective or not, and the theorem states that if $a \in f(U)$ is a regular value of $f$ , then $f^{-1} (a) $ is a regular surface in space.

But $f^{-1} (a)$ is a set of points such that $f(x,y,z) = a$ , my question is, what if $f$ is injective? Then $f^{-1} (a)$ must be a unique single value, and that single point cannot possibly be a regular surface, so what's wrong with my understanding?

khaled014z
  • 510
  • Nothing. It's just that differentiable functions from open subsets of $\Bbb R^3$ to $\Bbb R$ are never injective. –  May 20 '20 at 08:19
  • Is this a theorem? Where can I read about it? – khaled014z May 20 '20 at 08:26
  • Presumably further in your book. However, you've already argued that no value $a\in f(U)$ can be regular. Therefore, for all $x\in U$, $f^{-1}(f(x))$ must contain some $y$ such that $d_yf=0$ and since $f^{-1}(f(x))={x}$, it must be $y=x$. Specifically, $d_xf=0$ for all $x\in U$. You should have somewhere the result that $d_xf=0$ for all $x$ implies that $f$ is locally constant. –  May 20 '20 at 08:37

1 Answers1

1

Nothing wrong there. It's just that differentiable functions from open subsets of $\Bbb R^3$ to $\Bbb R$ are never injective. In fact, you've already argued that for an injective differentiable function $f:U\to\Bbb R$ no value $a\in f(U)$ can be regular. Therefore, for all $x\in U$, $f^{-1}(f(x))$ must contain some $y$ such that $d_yf=0$. Since $f^{-1}(f(x))=\{x\}$, it must be $y=x$. Specifically, $d_xf=0$ for all $x\in U$. You should have somewhere (I recommend reading your book, but here is an instance) the result that $d_xf=0$ for all $x$ implies that $f$ is locally constant (and therefore not injective).