I know how to integrate, but I can't understand how the integral of this fourier serie is calculated. my problem is with integral of the sigma.
fourier:
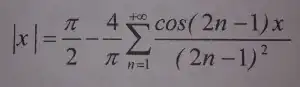
integral:
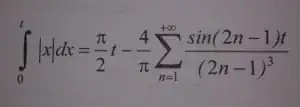
Can anyone say me how this integral is calculated?
I know how to integrate, but I can't understand how the integral of this fourier serie is calculated. my problem is with integral of the sigma.
fourier:
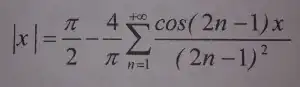
integral:
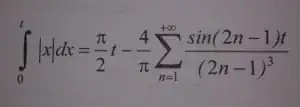
Can anyone say me how this integral is calculated?
Since $|\cos((2n-1)x)|\le 1$, the series is uniformly convergent and so you can exchange the order of integration and summation.
\begin{eqnarray} \int_0^t (\frac{\pi}{2}-\frac{4}{\pi} \sum_{n=1}^\infty \frac{\cos((2n-1)x)}{(2n-1)^2} )dx &=& \int_0^t\frac{\pi}{2} dx-\int_0^t \frac{4}{\pi} \sum_{n=1}^\infty \frac{\cos((2n-1)x)}{(2n-1)^2} dx \\ &=& \frac{\pi}{2}t - \frac{4}{\pi} \sum_{n=1}^\infty \int_0^t \frac{\cos((2n-1)x)}{(2n-1)^2} dx \\ &=& \frac{\pi}{2}t - \frac{4}{\pi} \sum_{n=1}^\infty \frac{\sin((2n-1)t)}{(2n-1)^3} \end{eqnarray}