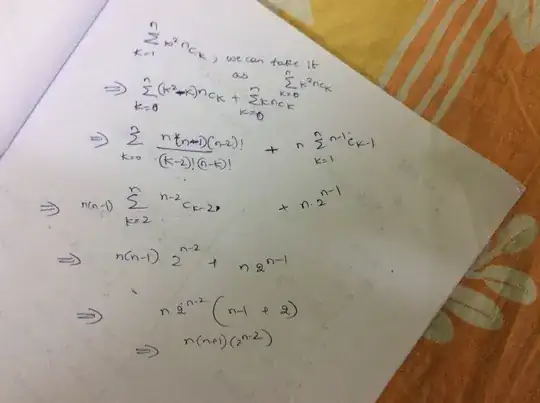Prove that $\sum_{k=1}^n k^2 \binom{n}{k}=n(n+1)2^{n-2}$

Question

I tried like this:

I used induction on $n$. I took $n=2$ then $LHS= \sum_{k=1}^2 k^2\binom{n}{k}=1\times 2+4\times 1=6$ and $RHS=2(2+1)=6$

and so its verified.

Now we assume that $\sum_{k=1}^n k^2 \binom{n}{k}=n(n+1)2^{n-2}$ is tue. We prove it for $n+1$.

Now $\sum_{k=1}^{n+1} k^2 \binom{n+1}{k}=\sum_{k=1}^n k^2 \binom{n+1}{k}+(n+1)^2$.

I cant know how to get $(n+2)(n+1)2^{n-1}$ from here.

Can someone please help me out?

I found an answer here https://math.stackexchange.com/a/231602/665065 which is the best and efficient. Thank you all for your effort

score 0 · Answer 1 · answered May 19 '20 at 13:42

0

Hint: Use $\binom{n+1}{k} = \binom{n}{k}+\binom{n}{k-1}$.

answered May 19 '20 at 13:42

DeepSea

77,651

Thank you but how to tackle the term $\sum_{k=1}^{n} k^2\binom{n}{k-1}$?? – Charlotte May 19 '20 at 13:47
@Math_Freak: write: $k^2 = (k-1)^2 +2(k-1) + 1$ – DeepSea May 19 '20 at 13:52
@Math_Freak: The one you have equals : $n2^{n-1}$ ( I think ). – DeepSea May 19 '20 at 13:56

score 0 · Answer 2 · answered May 19 '20 at 14:02

Combinatorial Proof

Counting in method $1$: We count the number of committees formed out of $n$ people with one president and one vice president with the condition that both president and vice president can be the same person. Number of such committees of size $k$ is $k^2\binom{n}{k}$(why?). So the total number of such committees is $\sum_{k=1}^{n}k^2\binom{n}{k}$.

Counting in method $2$: Now we chose a president first and a vice president and then the rest committee. When the president and vice president are the same then the number of such committees is $n2^{n-1}$(why?). When they are different people, the number is $n(n-1)2^{n-2}$(why?). So the total number of such committees is $n2^{n-1}+n(n-1)2^{n-2}=(2n+n(n-1))2^{n-1}=(2n+n^2-n)2^{n-1}=n(n+1)2^{n-1}$

Hence we get, $$\sum_{k=1}^{n}k^2\binom{n}{k}=n(n+1)2^{n-1}$$

Namburu Karthik · Answer 3 · 2020-05-19T14:00:17.623

-1

I don’t know how to type these sigma function so I posted written one

edited May 19 '20 at 14:00

answered May 19 '20 at 13:46

Namburu Karthik

329

2

Try to post LaTeX edited post – ShBh May 19 '20 at 13:49
1

I appreciate your effort but unfortunately I dont get the third line, also why do you write "implies " when there is no RHS – Charlotte May 19 '20 at 13:51
1

Start learning LaTeX. – Alapan Das May 19 '20 at 13:59
I edited it. Sir – Namburu Karthik May 19 '20 at 14:00
You can find a tutorial on typing math on this site here: https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference (Technically, it's "MathJax".) It's worth learning. – awkward May 19 '20 at 14:13
You have to write \sigma when this enclosed with two $ on both sides. – Alapan Das May 19 '20 at 14:40

Prove that $\sum_{k=1}^n k^2 \binom{n}{k}=n(n+1)2^{n-2}$

3 Answers3