Constructing a Transition Function Satisfying Additional Constraints

Question

The problem: I'm looking to construct a smooth function $f(x)$ for $x\in[0, 1]$ that satisfies the following simple constraints $$f(0)=1$$ $$f(1)=0$$ $$f'(0)=f'(1)=0$$

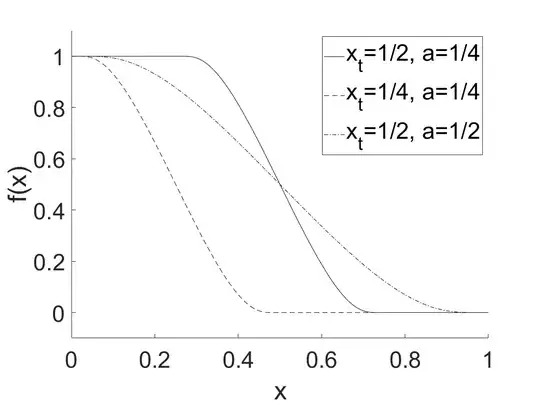
as well as the following general "transition" constraints $$f(x_t)=1/2$$ $$0\geq f'(x)\geq-s$$ $$f'(x_t)=-s$$

Here, $x_t\in(0, 1)$ is loosely a "transition" point where the transition from $f(0)=1$ to $f(1)=0$ is halfway done and "strongest" in a sense, controlled by the slope $s$.

My work so far: An example of such a function for $x_t=1/2$ and $s=\pi/2$ is

$$f(x)=\frac{1}{2}(1+cos(\pi x)).$$

However, I wish to primarily control $x_t$ while keeping a constant $s\geq1$ for a sufficiently "sharp" transition. The simple constraints above suggest a transition function (like the ones here) may be appropriate, but I can't work out one that also satisfies the general transition constraints. An approximate function can be constructed with a hyperbolic or inverse tangent function, such as

$$f(x)=\frac{1}{2}\left(1-\tanh\left(2s(x-x_t)\right)\right)$$

This satisfies the general transition constraints, but only approximately satisfies the the simple constraints for sufficiently large $s$. Because I will be varying $x_t$, the value of $s$ would need to be quite large to be sufficient. Therefore, I would prefer a function that exactly satisfies all the constraints.

I would appreciate any help constructing such a function! A simple closed form would be ideal, but I only need to be able to numerically evaluate the function for a set of points in $[0,1]$.

Answer 1

In formally writing down the constraints on $f'(x)$, I realized they're precisely those of a bump function. With this, I managed to construct an appropriate function $f(x)$:

$$f(x)=\begin{cases}1 & x\leq x_t-a \\ 1-\frac{1}{aI}\int_{x_t-a}^x\exp\left(\frac{1}{\left(\frac{x-x_t}{a}\right)^2-1}\right)\,dx & |x-x_t|<a \\ 0 & x\geq x_t+a\end{cases}$$

where

$$I=\int_{-1}^1\exp\left(\frac{1}{x^2-1}\right)\,dx.$$

This is constructed by letting $f'(x)$ be a bump function over the interval $(x_t-a,x_t+a)$ and integrating to retrieve $f(x)$. We can see that $f(x)$ is differentiable, and $f'(x)$ is a bump function. Thus $f(x)$ is smooth. Furthermore, $f(x_t)=1/2$ as desired, and the resulting slope is

$$f'(x_t)=\frac{1}{aeI}=s.$$

So, to control $s$ we set $a=1/seI$. One restriction to be aware of is that we must have $a\leq x_t$, giving the bound

$$s\geq\frac{1}{x_teI}.$$

Let me know if I've made any mistakes here. I would also like to see any other functions that satisfy the constraints.