Context
I'm trying to wrap my head around the measure-theoretic definition of a random variable. I put forward this example in the hopes that someone can verify that my understanding is correct, or else indicate how it is incorrect.
I have done a non-exhaustive search on this site. I have found 1 helpful, but it still does not give me full comprehension.
Problem
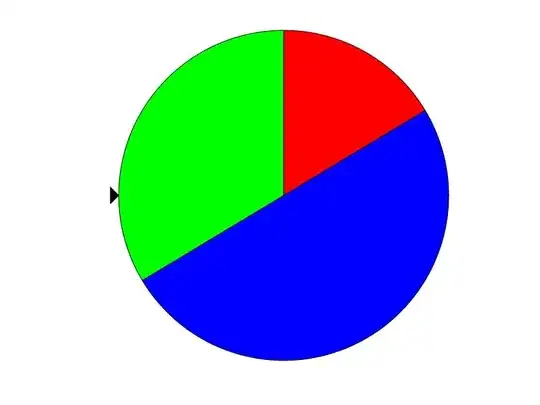
In the figure below, I offer a circular wheel with uniform density. The experiment is to spin the wheel and record what color is aligned with the rightmost vertice of the black triangle.
By $\Omega$, I denote the sample space, which I enumerate with three outcomes as $$\Omega = \left\{\text{red}, \text{blue}, \text{green} \right\}.$$
By $\mathcal{F}$, I denote the $\sigma$-algebra, which I enumerate with $2^3$ events as $$\mathcal{F} = \left\{\varnothing, \left\{\text{red}\right\}, \left\{\text{blue}\right\}, \left\{\text{green}\right\}, \left\{\text{red}, \text{green}\right\}, \left\{\text{red}, \text{blue}\right\}, \left\{\text{green}, \text{blue}\right\}, \left\{\text{red}, \text{green}, \text{blue}\right\} \right\}.$$
By $P$, I denote the probability measure, which I enumerate \begin{align} P(\varnothing) &= 0, \\ P(\left\{\text{red}\right\}) &= 1/6, \\ P(\left\{\text{blue}\right\}) &= 3/6, \\ P(\left\{\text{green}\right\}) &= 2/6, \\ P(\left\{\text{red}, \text{blue}\right\}) &= 4/6, \\ P(\left\{\text{red}, \text{green}\right\}) &= 3/6, \\ P(\left\{\text{green}, \text{blue}\right\}) &= 5/6,~\text{and} \\ P(\left\{\text{red}, \text{green}, \text{blue}\right\} ) &= 6/6. \end{align}
By the triplet $(\Omega ,{\mathcal {F}},P)$, I denote the probability space.
By $E$, I denote the set $\left\{1,2,3\right\}.$
By $\mathcal{E}$, I denote a $\sigma$-algebra that I give as $$\mathcal{E} = \left\{\varnothing,\{1\},\{2,3\},\{2\},\{1,3\},\{3\},\{1,2\}, \{1,2,3\}\right\}.$$
By the tuple $(E ,{\mathcal {E}})$, I denote the measurable space.
By the measurable function $ X\colon \Omega \to E$, I denote an $(E,{\mathcal {E}})$-valued random variable that I define as \begin{align} X(\omega) = \begin{cases} 1,&~\text{if}~\omega = \text{red}; \\ 2,&~\text{if}~\omega = \text{blue};~\text{or} \\ 3,&~\text{if}~\omega = \text{green}. \end{cases} \end{align}
For every subset $B\in {\mathcal {E}}$, I denote its preimage as $X^{-1}(B)$, where $X^{-1}(B)=\{\omega :X(\omega )\in B\} $.
I want to check that for every subset in $\mathcal {E} $, its preimage $X^{-1}(B)$ is in $\mathcal {F}$.
\begin{align} X^{-1}(\varnothing) &= \{\omega : X(\omega)\in \varnothing\} = \varnothing \\ X^{-1}(\{1\}) &= \{\omega : X(\omega)\in \{1\}\} = \{\text{red} \} \\ X^{-1}(\{2\}) &= \{\omega : X(\omega)\in \{2\}\} = \{\text{blue} \} \\ X^{-1}(\{3\}) &= \{\omega : X(\omega)\in \{3\}\} = \{\text{green} \} \\ X^{-1}(\{1,2\}) &= \{\omega : X(\omega)\in \{1,2\}\} = \{\text{red},\text{blue}\} \\ X^{-1}(\{1,3\}) &= \{\omega : X(\omega)\in \{1,3\}\} = \{\text{red},\text{green} \} \\ X^{-1}(\{2,3\}) &= \{\omega : X(\omega)\in \{2,3\}\} = \{\text{blue},\text{green} \} \\ X^{-1}(\{1,2,3\}) &= \{\omega : X(\omega)\in \{1,2,3\}\} = \{\text{red},\text{blue},\text{green} \} \end{align}
Biibliography