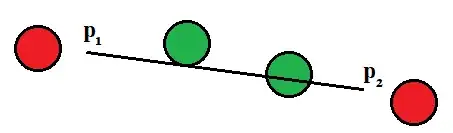
I have 2 points $p_1$ and $p_2$ in a $2D$ plane. There are $N$ balls of radius $r$ scattered in the plane. I want to know which balls will be crossed by the segment $p_1 \rightarrow p_2$.
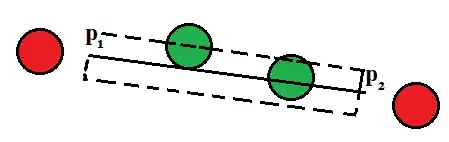
I did it using line-point distance, but obviously, when checking the balls, some of them who are not crossed by the segment are giving me false-positives, since they are crossed by the line formed from the points $p_1$ and $p_2$.
Given $p_1$, $p_2$, $r$ and the position $(x,y)$ of a ball, how can I know if this ball is crossed by the segment?
In the image below, the green balls are crossed while the reds are not.