5

$X$ and $Y$ are i.i.d. $N(0,1)$ random variables. You are given that $Y >0$. What is the probability that $Y>3X$?

Solution. The key is that $N(0,1)^2$ is cyclically symmetric. When plotting the distributions,the pdf will be cyclically symmetric about the origin. Then one can perform a geometric probabiltiy calculation to obtain the answer.

How is $N(0,1)$ cyclically symmetric? Im not sure what this means in this case.

How does $Y>0$ change this question? When you dont have this you can just consider adding multiple of the normal distribution (ie considering $Y-3X$)

Community
  • 1
Trajan
  • 5,194
  • 2
  • 27
  • 71
  • Can you tell us what a "geometric probability calculation" means to you? What is the context of this question? Does this solution come from a particular book or source? (One can certainly reduce this question to an "orthant probability" for a 2-variable normal distribution, but it's unclear what sort of answer will be most helpful to you.) – Greg Martin May 12 '20 at 14:59
  • This is a strange "solution". A standard way to do so would be to write this as a a double integral and use polar coordinates. The fact that $Y > 0$ means that instead of considering $Y$ to be standard normal, it should be standard normal conditioned to be positive, that is, with density $\frac{2}{\sqrt{2 \pi}} e^{-y^2/2} 1_{{y>0}}$. – Raoul May 12 '20 at 15:00
  • Isn't the question about computing $P(Y>3X,\mid, Y>0)$? In what sense would that be the same as computing $P(Y>3X)$? – md5 May 12 '20 at 15:00
  • @GregMartin https://www.math.lsu.edu/~smolinsk/Quant_Interview_Prep.pdf page 14, question 4 – Trajan May 12 '20 at 15:01
  • 2
    My understanding of that is that $N(0,1)^2$ is a two-dimensional normal, and "geometric" does not refer to a geometric distribution, but to doing geometry... – Raoul May 12 '20 at 15:03

2 Answers2

8

The "cyclical symmetry" is referring to the joint probability distribution of $X$ and $Y$, which is a bivariate normal distribution. We won't actually need any details of the distribution or its pdf (if this is something you haven't seen before, it is easy to look up), asides from the important fact that it has rotational symmetry about the origin (see the image below):

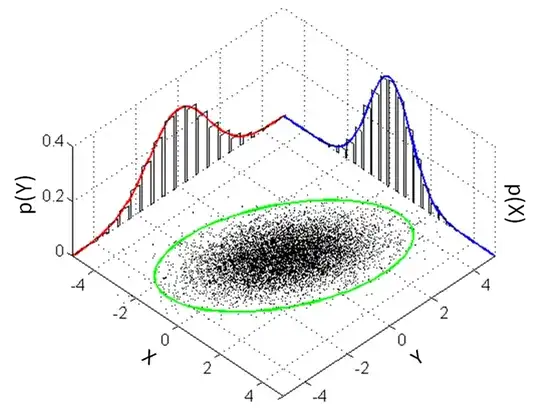
enter image description here

(Note: The image just shows a general bivariate normal distribution; in our case, imagine that it is perfectly cylindrically symmetric about the origin.)

Now the condition $Y>0$ means that we are restricting ourselves to the upper half-plane (i.e. the conditional distribution is the same as the image above, but restricted to the upper half plane). The condition that $Y > 3X$ (given that $Y > 0$) means that we want to find the probability that a random point in the $y>0$ half-plane lies in the sector between the line $y = 3x$ and the negative $x$-axis.

But by exploiting the rotational symmetry, this probability is just $\theta/\pi$ where $\theta$ is the angle between the line $y=3x$ and the negative $x$-axis. That is, $P(Y>3X \mid Y>0) = \frac{\frac{\pi}{2} + \arctan(1/3)}{\pi} \approx 0.602$.

I have purposely not been too precise with exactly what the relevant density functions and conditional density functions are, as I believe this is in the spirit of the "geometric" argument that was asked for. Of course, this is all easy to make precise by simply writing down the relevant probability density functions and converting to polar coordinates.

John Don
  • 1,179
  • 2
    Given that $Y>0$, it seems like that would mean $Y>3X$ whenever $X<0$, which is half the time (plus sometimes when $X>0$). So shouldn't the answer be more than $0.5$? I may be mossing something .. I often am. – Ned May 12 '20 at 18:19
  • 2
    I am getting the probability $\frac12+\frac1{\pi}\arctan(\frac13)$ from here. – StubbornAtom May 12 '20 at 20:31
  • 1
    @Ned You are right! I have written $Y>0$ but the condition I have actually been (mistakenly) using is $X > 0$! – John Don May 13 '20 at 17:46
  • 1
    @StubbornAtom You are correct! I mistakenly used the condition $X>0$ instead of $Y>0$ (even though I correctly wrote $Y>0$ in the answer). I have corrected this now. – John Don May 13 '20 at 17:51
1

Not sure what cyclically symmetric means, but if it means that the distribution is symetric wrt any line that goes through the origin it also means that its plot is stable under any $(0,0)$-centered rotation. Therefore the probability is $1/2$ (basically slice the density in half).

It may be easier just to notice that $U=Y-3X$ is normal with mean $0$ and variance $1^2+3^2=10$, therefore $P(U>0)=1/2$.

If in addition you condition on $Y>0$ you can basically treat the distribution like a pie-chart and get $P(Y>3X)$ as a ratio of some angle to the half circle $\pi$ (probably involves $\arctan 3$).

A.G.
  • 2,781