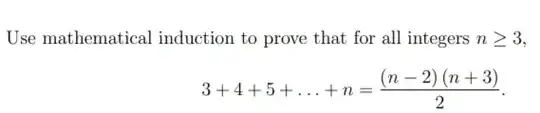I have proved for n =3, and assumed S(k) is true already.
I have gotten all the way to the induction step of S(k+1) = 3+4+5+...+(k+1) = ((k+1-2)(k+1+3))/2
I am having trouble proving it past this step, and how to show that what I have added is equal on both sides. Please show me how I can do that last step of showing the truth.