1

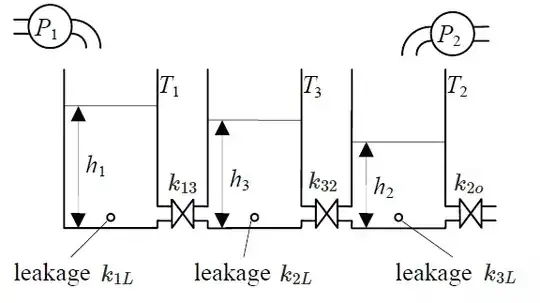
This question is very closely related to another question previously asked here on Math Stackexchange, where linearization of a three-tank-system is discussed.

enter image description here

After linearization you would get at multiple lines factors of the form $\frac{h_1 - h_3}{2|h_1 - h_3|^{\frac{3}{2}}}$, where $h_i$ denotes the water level in a certain tank $i$. A common control objective is to bring the water level of all three tanks to a certain height, but wouldn't this result in a singularity where the denominator is going to zero, and thus the entire fraction going to infinity?

My question is: Is this a problem when trying to control the water level in all three tanks, and if it is, is there a way around this?

MartijnKor
  • 27

1 Answers1

1

The dynamics can't be approximated well with a linearization near $h_1 = h_2 = h_3$ for a similar reason why the Maclaurin series of $\sqrt{|x|}$ doesn't exists. Namely, because the derivative near $x=0$ is not well defined. However, linearization should work if when you use $h_1 \neq h_3$ and $h_3 \neq h_2$ as an operating point.

If you still want to steer the system towards $h_1 = h_2 = h_3$ you would have to resort to nonlinear control.

Kwin van der Veen
  • 11,858