0

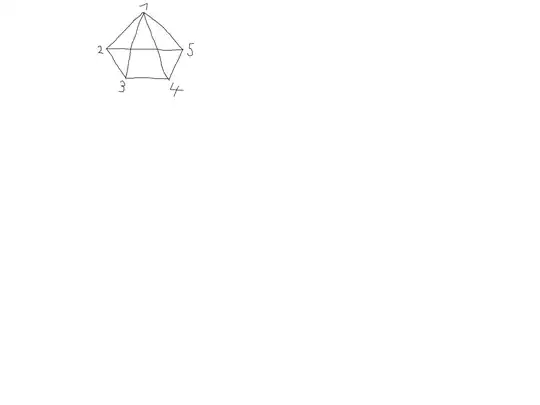
I am working on the following exercise:

Below is the transition graph of a Markov chain $(X_n)_{n \ge 0}$ where each edge is bi-directional . For each vertex, the probabilities of the out-going edges are uniformly distributed, e.g. the probability of moving from 1 to 3 is 1/4 and from 2 to 5 is 1/3 .

a) Find the stationary distribution.

b) Compute the entropy rate of the stationary Markov chain.

c) Compute the mutual information $I(X_n; X_{n−1})$ assuming the process is stationary.

enter image description here

My attempt:

a) The first thing I did was writing down the transition matrix $P$ as:

$$ \begin{pmatrix} &0 &1/4 &1/4 &1/4 &1/4 \\ &1/3 &0 &1/3 &0 &1/3 \\ &1/3 &1/3 &0 &1/3 &0 \\ &1/3 &0 &1/3 &0 &1/3 \\ &1/3 &1/3 &0 &1/3 &0 \\ \end{pmatrix}$$

And I computed the stionary distribution $\nu$ as the left eigenvector of $1$ from $P$ as

$$\begin{bmatrix} 0.5547 &0.4160 &0.4160 &0.4160 &0.4160 \end{bmatrix}.$$

b) For the entropy rate I would just use the formula

$$-\sum_{x,y \in \mathcal{X}} \nu(x) \ p(y \mid x) \ \log_2(p(y \mid x)).$$

c) I do not know what to do here. What should "stationarity" help in computing mutual information? Could you explain this point to me?

Community
  • 1
3nondatur
  • 4,178

1 Answers1

1

Until the Markov chain reaches the stationary state, the probability distribution keeps changing, so a time-invariant mutual information does not make sense. That is, you can't find an expression to just plug in a value of $n$ and get the mutual information.

Let $\pi = \{\pi_i\}_{i=1}^5$ denote the stationary distribution. Then, \begin{align*} I(X_n; X_{n-1}) &= H(X_n) - H(X_n|X_{n-1}) = H(\pi) - H(X_n|X_{n-1}) \end{align*}

$H(\pi)$ is easy to compute, so we just need to figure out how to deal with the second term. Luckily, that's already done in the previous part. Letting $H(\mathcal{X})$ denote the entropy rate of the chain, here is a quick derivation: \begin{align*} H(\mathcal{X}) &= \lim_{n \to \infty} \frac{1}{n}H(X_1,...,X_n) \\ &=^{(1)} \lim_{n\to \infty} \frac{1}{n} \sum_{i=1}^n H(X_i|X_{i-1},...,X_1) \\ &=^{(2)} \lim_{n\to \infty} H(X_n|X_{n-1},...,X_1) \\ &=^{(3)} \lim_{n\to\infty} H(X_n|X_{n-1}) \\ &=^{(4)} H(X_n|X_{n-1}) \end{align*}

(1) By Chain Rule, (2) By Cesàro convergence, (3) By Markovianity, (4) By stationarity, i.e. since the distribution has already converged to its limit, so has this expression.

Putting it all together, $$I(X_n; X_{n-1}) = H(\pi) - H(\mathcal{X}).$$

curlycharcoal
  • 700
  • 4
  • 11