Understanding the column space

Question

I am learning linear algebra from 3b1b series.

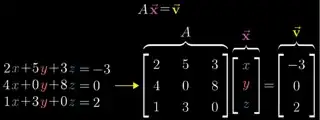
At this point, he explains for what he is using variables $A, \vec{x}$ and $\vec{y}$:

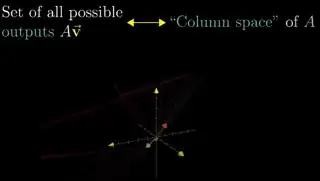
Then at here, he says:

P1:

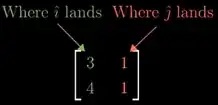
he further says following:

Set of all possible outputs of matrix, whether it’s a line, a plane or a 3D space, whatever, is called the column space of your matrix. The column of matrix tell whether the basis vectors land:

P2: Span of those transformed basis vectors gives all possible outputs.

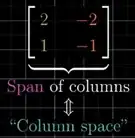
P3: In other words, the column space is the span of the columns of your matrix.

(Note that all above $2\times 2$ matrices are different examples of $A$.) Now the author of videos has taken unit direction vectors as basis throughout his videos:

$\hat{i} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \hat{j} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \hat{k} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} $
So to get corresponding tranformed vectors, we will put $\vec{x}=\hat{i},\vec{x}=\hat{j}$ and $\vec{x}=\hat{k}$ in $A\vec{x}=\vec{y}$

Lets say we get,
$A\hat{i}=\vec{I}$,
$A\hat{j}=\vec{J}$,
$A\hat{k}=\vec{K}$

Then, I feel its set of all vectors obtained by linear combinations of $\vec{I},\vec{J}$ and $\vec{K}$ is called column space of $A$. That is,

P4: column space $=\{\vec{V}|\vec{V}=c_1\vec{I}+c_2\vec{J}+c_3\vec{K}\}$

Q1. Am I correct with above?

Q2. If yes is answer to Q1, then how $\{\vec{V} | ..\}$ in P4 is same as $A\vec{v}$ in P1? Specifically, P4 does not involve $A$, but P1 does involve $A$ (,though I can understand $\vec{V}$ is somewhat same as / related to $\vec{v}$).

Q3. Geometrically $A$ defines a transformation. Then why it calls "Column space of $A$" in P1 and "span of the columns of your matrix" in P3, when as per P4 (if at all P4 is correct), column space is a space formed by linear combination of $\vec{I},\vec{J}$ and $\vec{K}$?

Q4. My general understanding about column space, after reading various definitions online, is that its a set of all vectors (range or image) obtained by applying $A$ to all vectors in given/current vector space (domain). Thus it is range / image of function defined by transformation $A$. Am I correct with this?

Answer 1

$A\vec{x}$ is a linear combination of the columns of $A$, with the coefficients coming from $\vec{x}$ (this follows from the definition of matrix multiplication). In the example above, the multiplication $$\begin{bmatrix} 2 & 5 & 3\\ 4 & 0 & 8\\ 1 & 3 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}$$ is the same thing as $$x \begin{bmatrix} 2\\4\\1 \end{bmatrix} + y \begin{bmatrix} 5\\0\\3 \end{bmatrix} + z \begin{bmatrix} 3\\8\\0 \end{bmatrix}.$$

If we look at it this way, we see how the range/image is equal to the span of the columns (i.e. the column space): $$ \text{range of $A$} = \{ A\vec{x}: \vec{x} \in \mathbb{R}^{3} \} = \{ \begin{bmatrix} 2 & 5 & 3 \\ 4 & 0 & 8\\ 1 & 3 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}: x, y, z \in \mathbb{R} \} = \{ x \begin{bmatrix} 2\\4\\1 \end{bmatrix} + y \begin{bmatrix} 5\\0\\3 \end{bmatrix} + z \begin{bmatrix} 3\\8\\0 \end{bmatrix}: x, y, z \in \mathbb{R} \} = \text{column space of $A$} $$

You can see how this generalizes to any matrix and any vector.

Edit: to answer your "P4": with the view of matrix-vector multiplication as a linear combination of columns, you can see that $A\hat{i}$ is just the first column of $A$; $A\hat{j}$ the second column; and $A\hat{k}$ the third column. So, yes, the column space is $\{ \vec{V} \mid \vec{V} = c_1\vec{I} + c_2\vec{J} + c_3\vec{K} \}$.

In other words, the columns of $A$ are the transformed standard basis vectors, and the column space is the set of all linear combinations of these transformed vectors. So, in $\mathbb{R}^3$ for example, you can determine what a matrix does just by computing what it does to $\hat{i}, \hat{j}$, and $\hat{k}$. Then for any vector $\vec{x} = \begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix} = x_1\hat{i} + x_2\hat{j} + x_3\hat{k}$ in $\mathbb{R}^3$, $A\vec{x}$ is just $x_1 A\hat{i} + x_2A\hat{j} + x_3A\hat{k}$. This can be seen to be true by linearity, or by the view as described earlier of matrix-vector multiplication as a linear combination of the columns.

Answer 2

Regarding Q1: Yes, you are correct.

Regarding Q2: in a sense, this is the entire point of linearity. In particular, if $\vec v = c_1 \vec i + c_2 \vec j + c_3 \vec k$, then $$ A\vec v = A(c_1 \vec i + c_2 \vec j + c_3 \vec k) = c_1 A\vec i + c_2 A \vec j + c_3 A \vec k = c_1 \vec I + c_2 \vec J + c_3 \vec K. $$ So, if you know the vectors $\vec I,\vec J, \vec K$ (the images of $\vec i, \vec j, \vec k$), then every possible "output" $A\vec v$ can be written in the form $\vec V = c_1 \vec I + c_2 \vec J + c_3 \vec K$.

Another way to think about this: you said that your definition in P4 "doesn't involve $A$". However, by using $\vec I,\vec J, \vec K$, we have recovered all the information about the transformation associated with $A$.

Q3: As we established, these are two valid ways of describing the column space.

Q4: Yes, the column-space is the image of the transformation associated with $A$.