0

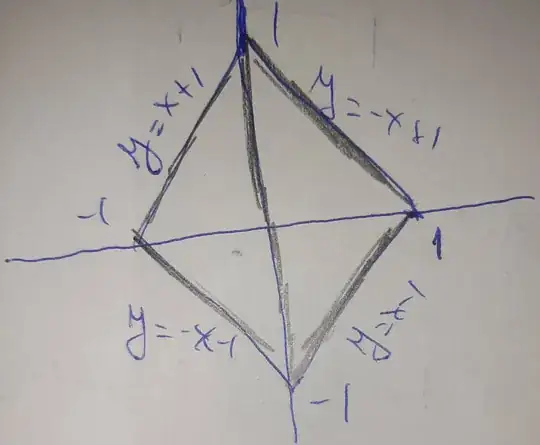
Giveing that I have a squere formed with the points (1,0) , (0,1) , (-1,0) , (0,-1) so basically a romb centerd in O(0,0) how do I find the domain of integration D ? I've started by giving the x his domain ( -1 < x < 1 ) and getting the equations for each side of the romb , as I wrote them in the image , but now I am stuck ... I want to get a domain for y using the variable x . enter image description here

VlAd TbK
  • 55

1 Answers1

0

It is $\int_0^{1}\int_{x-1}^{1-x} dydx+\int_{-1}^{0} \int_{-x-1}^{x+1} dy dx$ or $\int_{-1}^{1} \int_{|x|-1}^{1-|x|} dydx$.

Kavi Rama Murthy
  • 311,013
  • And if i wanted to have only 1 integral from -1 < x < 1 what would the domain of y look like ? – VlAd TbK May 03 '20 at 11:51
  • 1
    Just draw vertical lines. For example when $0<x<1$ the $y$ coordinate ranges from $y=x-1$ on the edge of the rhombus below the $x-$ axis to the $y=1-x$ on the edge of the rhombus above the $x-$ axis. Basically you have to fix an $x$ and look at the possible values for $y$. – Kavi Rama Murthy May 03 '20 at 11:52
  • If you want to avoid splitting the interval $(-1,1)$ you can write $\int_{-1}^{1} \int_{|x|-1}^{1-|x|} dydx$. – Kavi Rama Murthy May 03 '20 at 11:55