3

I saw nice geometric proof of $\sin{(x + y)} = \sin{x}\cos{y} + \sin{y}\cos{x}$ using unit circle. But I can't find proof when $x + y > 90^\circ.$

Is there intuitive, "simple" or geometric way to prove this? Can we maybe transform unit circle or what is going on here?

Quanto
  • 97,352
1b3b
  • 1,276
  • 2
    What have you tried? What fails in the prior proof when $x+y > 90^\circ$? – David G. Stork May 01 '20 at 17:52
  • 3
    By reflection, we have $\sin(90^{\circ}+a)=\sin(90^{\circ}-a)$ and $\sin(180^{\circ}-a)=\sin(a)$. So you can always transform it back to the known case. – Integrand May 01 '20 at 17:53
  • 1
    All identities outside of the first quadrant can be manipulated using either the related angle identities or the complementary angle identities. – Andrew Chin May 01 '20 at 17:55
  • What about using Ptolomeo's theorem? – Mystery May 01 '20 at 17:56
  • Because the stacking right triangles one on another is not possible for, say, $\sin {(100 ° + 120 °)}$. All proofs shows the situation for angles $x, y < 90^\circ$ (for example, $\sin{(30 ° + 45 °)}$. – 1b3b May 01 '20 at 17:58
  • @Integrand, I feel that is good way but can you systematically prove it for me in not-brute-force way. I always find myself stucked. Thanks – 1b3b May 01 '20 at 18:01
  • @Mystery, thanks I will search for that one. – 1b3b May 01 '20 at 18:03
  • 1
    The addition formulas are true for general angles because of the Principle of the Analytic Continuation. A proof of the formulas which doesn't need the condition $x + y < 90$ is the one using Ptolemy's theorem about the cyclic quadrilaterals. You can check Trigonometry by I.M Gelfand, He proves the formulas using Ptolemy's theorem in the appendix to Chapter 6, and talks about the Principle a bit at the Beginning of Chapter 7. – dude076 May 01 '20 at 18:30
  • Related (duplicate?): "Looking for an alternative proof of the angle difference expansion". In particular, my answer shows how to adapt my Wikipedia-famous diagram from this answer to a couple of non-acute cases. – Blue May 01 '20 at 23:46
  • @Blue, thanks but it seems to me that descripiton of aforementioned question requires only proofs from Euclidean geometry. I will certainly study your proof. – 1b3b May 02 '20 at 10:43
  • 1
    @1b3b When I teach this to my students I start by proving the formula for $\cos(\alpha-\beta)$ (which can be done geometrically for arbitrary angles), and from that the formula for $\sin(\alpha+\beta)$ can be derived, using $\sin(\alpha+\beta)=\cos(\pi/2-\alpha-\beta)$. – Intelligenti pauca May 02 '20 at 21:51
  • See this website – tryst with freedom Oct 04 '20 at 20:04

2 Answers2

2

Let $x$ and $y$ be any argument angles in the Argand diagram. Then, $ e^{i (x+y)} = e^{i x } e^{i y }$, or

$$\cos (x+y)+ i\sin(x+y) =(\cos x+i \sin x)(\cos y+i \sin y)$$

Match the real and imaginary parts to obtain

$$\cos(x+y)=\cos x\cos y-\sin x\sin y$$ $$\sin(x+y)=\sin x\cos y+\cos x\sin y$$

Quanto
  • 97,352
  • The only thing that is perhaps a little confusing here is the direction of the implications. I think it is more natural to prove $e^{i(x + y)}$ (#) using this basic trig identities (sine and cosine of the sum of angles) than vice versa (but I know that $e^{i(x + y)}$) can be proved by definition $e^{i\theta} = (1 + \frac{i\theta}{n})^n$ setting $\theta = x + y,$ and then of course (#) holds). Thanks for the nice trick, I didn't think of that! – 1b3b May 01 '20 at 22:39
2

Sorry I didn’t see this one earlier. When sitting in on high-school trigonometry classes, I’ve wondered about what the various proofs of sine addition might be, and which one might be the best. There is the purely geometric proof, which you know, but is no good for $x+y>90^\circ$. And there is the proof recommended by @intelligentipauca, involving a minimum of geometry but a great load of algebraic manipulation, and which ends up with no intuition on the student’s part. Here’s a proof that’s in between, involving a minimum of geometry, of trigonometry, and of algebra. It’s only good for $x<90^\circ$, similarly for $y$, but $x+y$ can be anything smaller than $180^\circ$.

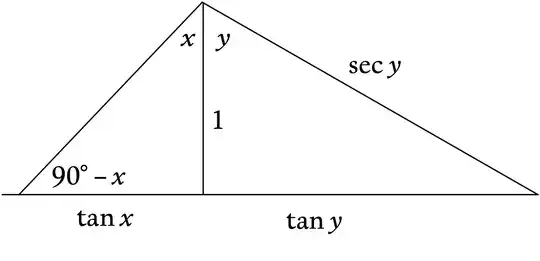
Start with a horizontal line, and erect a perpendicular segment on it, and call its length $1$. Draw angles $x$ and $y$ sharing the perpendicular, but on opposite sides, so that they make an angle of $x+y$ together. sine addition

Now you see that the two horizontal segments are $\tan x$ and $\tan y$, and that the right-hand hypotenuse is $\sec y$.

Next, call in the Law of Sines, according to which \begin{align} \frac{\sin(x+y)}{\tan x + \tan y}&=\frac{\sin(90^\circ-x)}{\sec y}\\ &=\cos x\cos y\,. \end{align} Now multiply both sides by $\tan x+\tan y$ and get $\sin(x+y)=(\tan x+\tan y)\cos x\cos y$. And there’s your addition formula for sines.

Lubin
  • 62,818