Let us define $\sin(x)$ as the solution to
$$y'' = -y$$
with initial conditions $y(0) = 0$ and $y'(0) = 1$. From this definition, we should be able to deduce from first principles that $\sin(x)$ is periodic, and reconcile this definition with the right-triangle definition of opposite over hypotenuse.
Any ideas on how to do this?
We rewrite the equation as a system: $$\tag{1} \left\{\begin{array}{rcl} y'&=&z\\ z'&=&-y. \end{array}\right. $$ The function $V(y,z)=y^2+z^2$ is a first integral of (1), i.e. it remains constant along the trajectories of(1). Indeed, its derivative along the trajectories is equal to zero: $$ \dfrac{dV(y(t),z(t))}{dt}=2yy'+2zz'=2yz+2z(-y)=0. $$ This implies that any solution $(y(t),z(t))$ of (1) (except for the only equlibrium point $y=z=0$) lies on a circle $y^2+z^2=R=\rm const$. For the solution that satisfies the initial conditions $y(0)=0$, $z(0)=1$ we have $R=y(0)^2+z(0)^2=1$.
Now look at the phase plane:
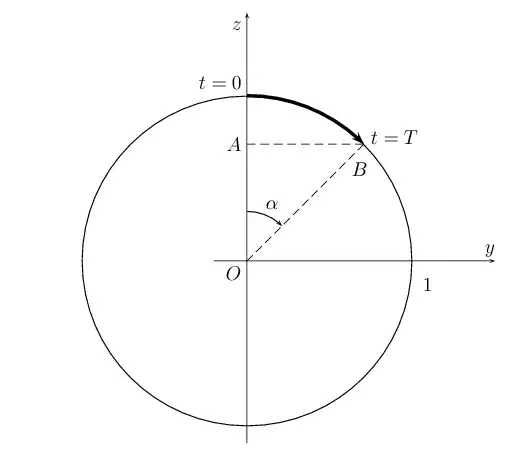
The solution that starts at the point $(0,1)$ moves clockwise because $y'(0)=z(0)=1>0$ (and it can't stop moving because the only equilibrium point is $(0,0)$). Let us express the length $l$ of the arc traversed by the solution along the circle when changing the parameter $t$ from $0$ to $T$ (the bold arc with an arrow on the picture). According to the curve length formula $$ l=\int_0^{T} \sqrt{(y'(t))^2+(z'(t))^2}\,dt= \int_0^{T} \sqrt{z^2+(-y)^2}\,dt= \int_0^{T} 1\,dt= T, $$ but $l=1\cdot \alpha=\alpha$, thus $\alpha=T$. This obviously implies that $y$ and $z$ are periodic with a period of $2\pi$.
Let $B$ be the point with coordinates $(y(T),z(T))$. The opposite over hypotenuse is $$ \sin\alpha=\frac{AB}{OB}=\frac{y(T)}{1}=y(T). $$
