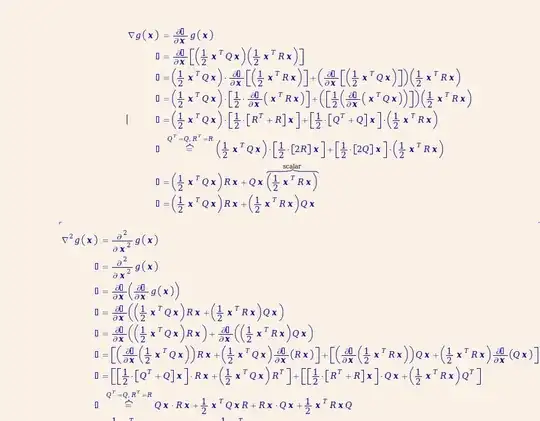The individual terms are easy to handle:
$$\eqalign{
\def\LR#1{\left(#1\right)}
\def\fracLR#1#2{\LR{\frac{#1}{#2}}}
\def\p{\partial}
\alpha &= \tfrac{1}{2}x^TQx,
\qquad \frac{\p\alpha}{\p x} &= Qx,
\qquad \frac{\p^2\alpha}{\p x\,\p x^T} &= Q
\\
\beta &= \tfrac{1}{2}x^TRx,
\qquad \frac{\p\beta}{\p x} &= Rx,
\qquad \frac{\p^2\beta}{\p x\,\p x^T} &= R \\
\\
}$$
The calculation for their product is straight forward:
$$\eqalign{
\pi &= \alpha\beta \\
\\
\frac{\p\pi}{\p x}
&= \beta\frac{\p\alpha}{\p x}
+ \alpha\frac{\p\beta}{\p x} \\
&= \beta Qx \;+\; \alpha Rx \\
\\
\frac{\partial^2\pi}{\p x\,\p x^T}
&= \beta\fracLR{\p^2\alpha}{\p x\,\p x^T}
+ \fracLR{\p\beta}{\p x} \fracLR{\p\alpha}{\p x^T}
+ \fracLR{\p\alpha}{\p x} \fracLR{\p\beta}{\p x^T}
+ \alpha\fracLR{\p^2\beta}{\p x\,\p x^T} \\
&= \beta Q \;+\; Rxx^TQ \;+\; Qxx^TR \;+\; \alpha R \\
}$$
Update
This update addresses ordering issues raised in the comments.
Differentials are often the best approach for matrix calculus problems because, unlike gradients, they satisfy a simple product rule:
$$\eqalign{
d(A\star B)
&= (A+dA)\star(B+dB) \;\;-\;\; A\star B \\
&= dA\star B + A\star dB \\
}$$
where
$A$ is a {scalar, vector, matrix, tensor},
$B$ is a {scalar, vector, matrix, tensor}, and
$\star$ is any product which is compatible with $A$ and $B.\;$ This includes the Kronecker, Hadamard/elementwise, Frobenius/trace and dyadic/tensor products, as well as the Matrix/dot product.
IFF the product commutes, you can rearrange the product rule to
$$d(A\star B) = B\star dA + A\star dB$$
The Hadamard and Frobenius products always commute. The other products are commutative only in special situations. For example the Kronecker product commutes if either $A$ or $B$ is a scalar, and the dot product commutes if both $A$ and $B$ are real vectors.
The differential and the gradient are related and can be derived from one another, i.e.
$$\frac{\p\alpha}{\p x} = Qx
\quad\iff\quad d\alpha = (Qx)^Tdx = x^TQ\,dx$$
Let's examine one of the terms in the preceding hessian calculation.
First calculate its differential, and then its gradient.
$$\eqalign{
y &= \alpha(Rx) = (Rx)\alpha
\qquad \big({\rm the\,scalar\star vector\,product\,commutes}\big) \\
dy &= \alpha(R\,dx) + (Rx)\,d\alpha \\
&= \alpha R\,dx \;\;\,+ Rx\;x^TQ\,dx \\
&= (\alpha R+Rx\,x^TQ)\,dx \\
\frac{\p y}{\p x} &= \alpha R+Rx\,x^TQ \\
}$$