Intuitive explanation of why $n \sum_{i=1}^n (x_i - x)^2 = \sum_{i< j} (x_i - x_j)^2$, where $x = \sum_{i=1}^n \frac{x_i}{n}$

Question

For real numbers $x_1, \dots, x_n$, we have the simple identity: $$ n \sum_{i=1}^n (x_i - x)^2 = \sum_{i< j} (x_i - x_j)^2$$ where $$x = \sum_{i=1}^n \frac{x_i}{n}$$
One can easily multiply out both sides to obtain the equality. Is there an easy way of seeing why this is true? Perhaps there is even a probabilistic reason since the left hand side resembles a variance.

Answer 1

Define a random variable $X$ such that $\mathbb{P}(X=x_i)=\dfrac{1}{n}$ for $1\leq i\leq n$. And take an I.I.D random variable $Y$.

So, \begin{align} \text{Var}(X)&=\frac{1}{2}\text{Var}(X-Y)\\ &=\frac{1}{n^2}\frac{1}{2}\sum_{i,j}(x_i-x_j)^2\\ &=\frac{1}{n^2}\sum_{i<j}(x_i-x_j)^2 \end{align} On the other hand $\text{Var}(X)=\frac{1}{n}\sum_{i=1}^n (x_i -\frac{1}{n}\sum x_j)^2$.

So, $$n\sum_{i=1}^n (x_i -\frac{1}{n}\sum x_j)^2=\sum_{i<j}(x_i-x_j)^2$$

Reference here.

Answer 2

Both sides of this identity are unchanged if you subtract a constant from each $x_i$, so you can just assume $x = 0$ and then what you want to show is that if the numbers sum to zero we have $$ n\sum_{i=1}^n x_i^2 = \sum_{i< j} (x_i - x_j)^2$$ Note that $$\sum_{i< j} (x_i - x_j)^2 = {1 \over 2}\sum_{i = 1}^n \sum_{j=1}^n (x_i - x_j)^2$$ $$= {1 \over 2} \sum_{i = 1}^n \sum_{j=1}^n x_i^2 + \sum_{i = 1}^n\sum_{j=1}^n x_i x_j + {1 \over 2} \sum_{i = 1}^n \sum_{j=1}^n x_j^2$$ $$= {n \over 2} \sum_{i = 1}^n x_i^2+ (\sum_{i = 1}^n x_i)(\sum_{j = 1}^n x_j) + {n \over 2} \sum_{j = 1}^nx_j^2$$ This equals $ n\sum_{i = 1}^nx_i^2$ since the sum of the $x_i$ are zero.

Answer 3

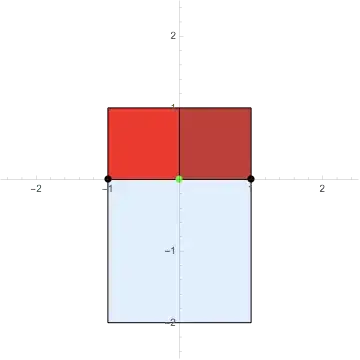
A start (visualizing squares):

Consider $n= 2$ and $x_1 = -1$, $x_2 = +1$ (and hence mean = $0$):

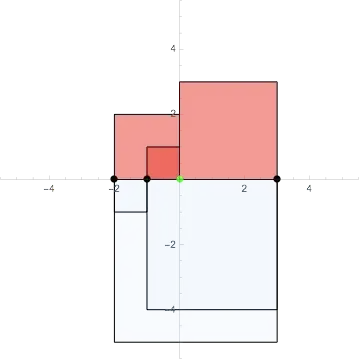
The points are in black, the mean in green, and the reddish area depicts one summation, the bluish area the other summation.

Now for $x_1=-2$, $x_2 = -1$, $x_3 = 3$ (and again, hence mean = $0$):