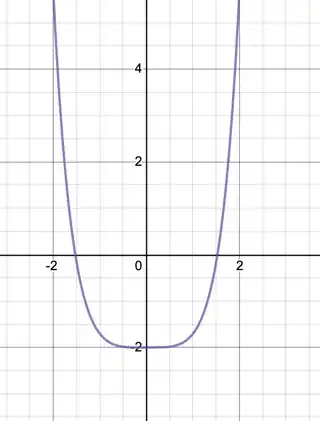
This seems to be a simple enough problem to find $x$, however there seems to be something missing $$f(x) = \sinh^2(x) - 2\cosh(x)$$ I know for a fact that there two $x$-intercepts for this function, as you can see here:
I tried using double angle formulas to change the terms into something easier to work with. This was just one of many approaches I tried, but failed at:
$\sinh^2(x) = \cosh(2x) - \cosh^2(x)$
$\cosh(2x) = 2 \cosh(x)^2 -1$
—> $2\cosh^2(x) - 1 - \cosh^2(x) - 2\cosh(x) = 0$.
And then I used a substitution for $\cosh(x)$ to find $x$, and I ended up with $$ x = \log\left(\sqrt{2}+1+\sqrt{2(\sqrt{2}+2)}\right) $$ as one of the answers, with the other $x$ value symmetric to it across the line $x = 0$. It was close, but incorrect. Would appreciate any help or guidance on what I should have been doing instead to get the answers I needed.