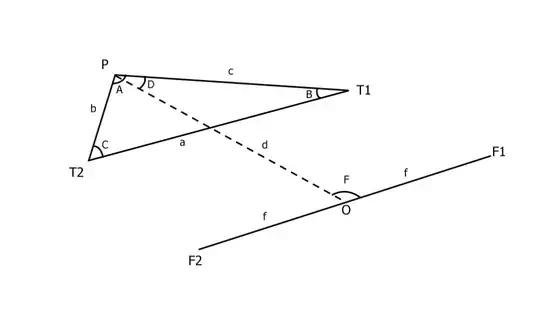
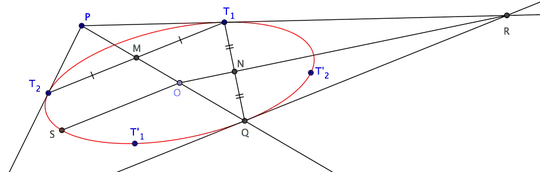
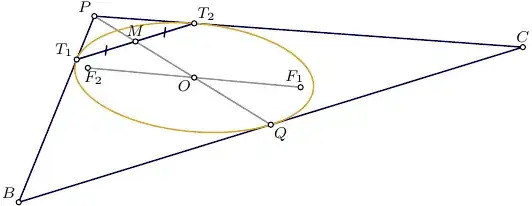
I like the more-geometric answers, but I'm somewhat committed to this analytic approach, so let's continue ...
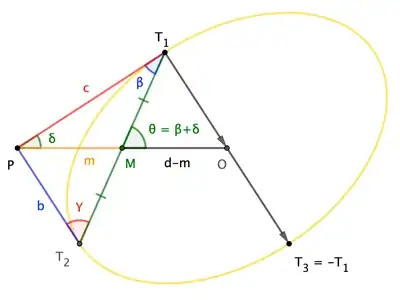
Place $O$ at the origin, and let $P = (-d,0)$. As @Aretino helpfully observes in a comment, $\overleftrightarrow{OD}$ must bisect the chord $\overline{T_1T_2}$, so define $M$ as midpoint of the chord, with $|PM|=m$, so that $M=(-d+m,0)$; also, define $\theta = \angle OMT_1 = \beta+\delta$. Then, with $a := |T_1T_2|$, we can write
$$T_1 = M + \frac{a}2(\cos\theta,\sin\theta) \qquad T_2 = M - \frac{a}2(\cos\theta,\sin\theta) \tag{1}$$
Since $O$ is the center of the ellipse, we can define, say, $T_3=-T_1$ to get a third point on the ellipse. Since $T_1$ and $T_2$ are points of tangency, we can tease them into double-points by defining
$$T_1' = T_1 + t_1(P-T_1) \qquad T_2' = T_2 + t_2(P-T_2) \tag{2}$$
for "infinitesimally small" $t_1$ and $t_2$ that we can treat as non-zero or zero as to our advantage.
With five points on the conic, we can use a determinant to get its equation. (See, for instance, this answer.) Using a computer algebra system such as Mathematica to expand the determinant, we obtain factors of $t_1$ and $t_2$ that we divide-out (because they're non-zero), then set the remaining instances of these values to $0$ (because they're not non-zero), so that the equation becomes ...
$$\begin{align}
0 &= x^2 a^2 \sin^2\theta
- 2 a^2 x y \cos\theta \sin\theta
+ y^2\left( 4 m (d-m) + a^2 \cos^2\theta \right) \\
&- a^2d\sin^2\theta \left( d - m \right)
\end{align}\tag{3}$$
From here, we can consult, say, this answer for recipes that express metric properties of a conic in terms of the coefficients of the general second-degree polynomial. We find that the angle $\phi$ that the major axis makes with the $x$ axis satisfies
$$\tan2\phi = \frac{a^2 \sin 2\theta}{4 (d - m) m + a^2 \cos 2\theta} \tag{4}$$
and the major and minor radii of the ellipse are given by
$$r_{\pm}^2 = \frac{d}{8m}\left( a^2 + 4m (d - m) \pm \sqrt{ a^4 + 16 m^2 (d - m)^2 + 8 a^2 m (d - m) \cos 2\theta )}\right) \tag{5}$$
To rewrite in terms of the problem's stated parameters, the Law of Cosines gives
$$a^2 = b^2 + c^2 - 2 b c\cos\alpha \tag{6}$$
where $\alpha := \angle T_1PT_2 = 180^\circ - \beta - \gamma$. We can use Stewart's Theorem to show
$$m^2 = \frac14\left(-a^2+2b^2+2c^2\right) = \frac14\left( b^2 + c^2 + 2b c \cos\alpha\right) \tag{7}$$
Also, since $|\triangle PT_1T_2| = \frac12b c \sin\alpha = \frac12am\sin\theta$, we can find
$$\begin{align}
\sin^2\theta &= \frac{4b^2 c^2 \sin^2\alpha}{(b^2+c^2-2b c\cos\alpha)(b^2+c^2+2b c \cos\alpha)} = \frac{4b^2c^2\sin^2\alpha}{(b^2-c^2)^2+4b^2c^2\sin^2\alpha} \tag{8} \\[4pt]
\cos^2\theta &= \frac{(b^2-c^2)^2}{(b^2-c^2)^2+4b^2c^2\sin^2\alpha} \tag{9} \\[4pt]
\cos2\theta &= \frac{(b^2-c^2)^2-4b^2c^2\sin^2\alpha}{(b^2-c^2)^2+4b^2c^2\sin^2\alpha} \tag{10}
\end{align}$$
Expressions $(4)$ and $(5)$ don't seem to get appreciably better by substituting-in from these expressions and simplifying (the arbitrary $d$ gets in the way), so I'll leave things here. $\square$