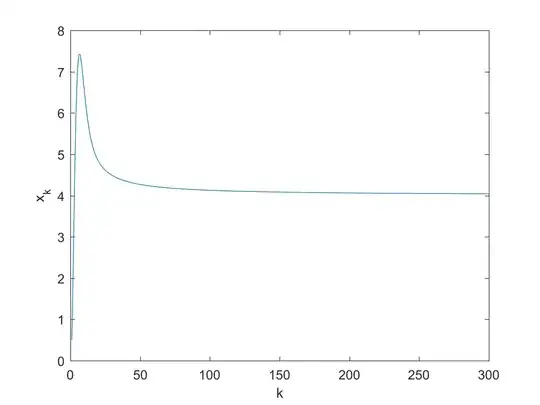
Consider the sequence $$ x_k = \frac{1}{2^k} \sum_{l=1}^k \left( \begin{array}{l}k\\l \end{array} \right) \left( \frac{k}{l}\right)^2,$$ where the first term in the sum is the binomial coefficient.
Question: Does this sequence converge or at least remain bounded?
I tried evaluating the limit with Mathematica without any luck. However, the numerical analysis below suggests that $x_k$ converge to a finite value (maybe 4?).
This is not an answer.
I suppose that Mathematica gave as a result $$x_k = \frac{1}{2^k} \sum_{l=1}^k \left( \begin{array}{l}k\\l \end{array} \right) \left( \frac{k}{l}\right)^2=2^{-k}\, k^3 \,\, _4F_3(1,1,1,1-k;2,2,2;-1)$$ which, I suppose, you could have computed for very large $k$.
Let $k=10^n$; computing $$\left( \begin{array}{cc} n & x_{10^n} \\ 1 & 6.53390898912372 \\ 2 & 4.12641241484375 \\ 3 & 4.01206038296720 \\ 4 & 4.00120060038029 \\ 5 & 4.00012000600038 \\ 6 & 4.00001200006000 \end{array} \right)$$ where you can see two nice patterns.
There was a comment, which contained the answer but seemed to have disappeared. Hence, I am posting this short answer myself.
In fact, one can use the approximating property of the Bernstein polynomials discussed in this earlier post defining the function $f$ to be $$f(x) = \left\{ \begin{array}{ll} x^{-2}, & x > \epsilon \\ \epsilon^{-2} & x \leq \epsilon \end{array} \right.$$ for some $\epsilon < \frac{1}{2}$