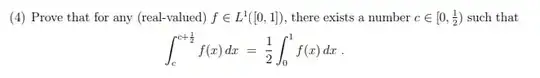2\int_{0}^{1}f(x)dx$

Asked Apr 18 '20 at 00:18

Active Apr 18 '20 at 00:18

Viewed 35 times

My attempt: Consider $$g(c)=\int_{c}^{c+1/2}f(x)dx$$g is continuous as $$g(c)=\int_{0}^{c+1/2}f(x)dx-\int_{0}^{c}f(x)dx$$ where both are continuous. Thus now we can use IVT to show such $c$ exists. Assume that $g(c)>1/2\int_{0}^{1}f(x)dx$ for all $c\in [0,1/2]$, but then $g(0)+g(1/2)>\int_{0}^{1}f(x)dx$ which is a contradiction. Thus $ g(c)\leq 1/2\int_{0}^{1}f(x)dx$ for some $c\in [0,1/2]$ if the equality holds from $c=1/2$ then it also holds for $c=0$. Otherwise by IVT we know such c exists.

Is this proof correct? Are there any cleaner solutions?

asked Apr 18 '20 at 00:18

Sorfosh

3,266

2

Looks fine. Nice proof! – Kavi Rama Murthy Apr 18 '20 at 00:27
1

Let $a=\int_{0}^{1}f(x),dx$ and apply universal chord theorem on $g(x) =\int_{0}^{x}f(t),dt-ax$ to get $g(c) =g(c+1/2)$ which gives the desired result. – Paramanand Singh Apr 18 '20 at 01:32
You could also use $\int_{a}^{b} f(x)dx = (b-a)\int_{0}^{1} f((b-a)x+a)dx$ – user600016 Apr 18 '20 at 06:34
Another proof, although similar, is obtained considering $h(c):=\int_c^{c+\frac12}f-\int_0^1f$ – Apr 18 '20 at 10:19

If $f \in L^1[0,1]$ then there exists $c \in [0,1/2)$ s.t $\int_{c}^{c+1/2}f=1/2\int_{0}^{1}f(x)dx$

0 Answers0