Selecting objects arranged in a circle - Solution Only By Counting

Question

I'm trying to understand the following solution (based on http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.96.8324).

Problem: What is the number of ways of selecting $k$ objects from $n$, which are arrayed in a circle and are not consecutive? (A different solution is at Choose K items from N in a circle)

Given Solution: There are $n$ choices for the first object selected. Next, we must select the remaining $\color{green}{k - 1}$ objects. In addition, to prevent consecutiveness, we must select the $\color{brown}{k}$ objects which lie between the $\color{green}{k - 1}$ objects.

Therefore, the number of objects UNaccounted for $:= U = (n - 1) - (\color{green}{k - 1} + \color{brown}{k}) = n - 2k$. We can only place these $U$ objects in between the selected $\color{brown}{k}$ objects, so the number of possible positions for these $U$ objects is $\color{brown}{k}$.

Therefore, the number of ways to select these $U$ positions = $\left( \begin{matrix} { k - 1 + U} \\ {U} \\ \end{matrix} \right)$. (Rest of soln omitted).

I don't understand this last sentence. I understand that we are choosing $U$ objects, but how are we choosing from $(k - 1 + U)$? Where did this number come from?

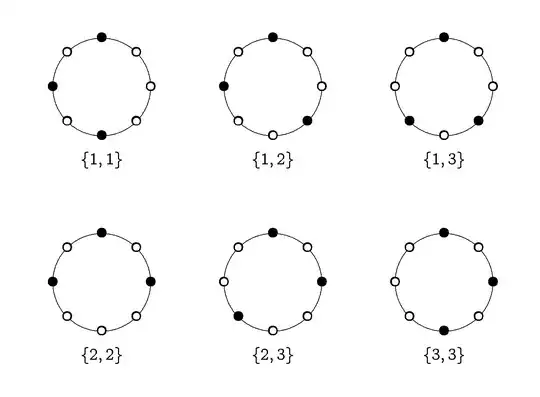
As a recourse to the general case, I appealed to the simpler case where $n = 8$ and $k = 3$. Then $U$ = 2 and the number of ways to select these $U$ positions = $\left( \begin{matrix} { 4} \\ {2} \\ \end{matrix} \right)$. But I can't see where 4 comes from either (We need to place U1 and U2 so I understand why we're choosing 2.). Here's my picture, where green denotes the $\color{green}k$ selected objects and black denotes the objects unaccounted for:

---

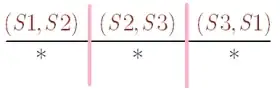
In response to Prof Scott's post, I thought to add that the bars in the stars-and-bars analogy aren't actually the $\color{brown}{\text{brown separators}}$ drew above. The bars, which I draw in pink below, actually separate the intervals between the $\color{brown}{\text{brown separators}}$. Pictorially:

Answer 1

It’s just a stars-and-bars calculation. You have $\color{brown}k$ separators arranged in a circle, so they define $k$ gaps between neighboring separators. You have $U$ objects to place arbitrarily in those $k$ gaps. This can be done in

$$\binom{U+k-1}{k-1}=\binom{U+k-1}U\tag{1}$$

ways. The justification for this result in the linked article is reasonably clear, but I’ll sketch it here. Break the circle at the first separator and stretch it out into a line. Then the $U$ objects and the remaining $k-1$ separators form a string of $U+k-1$ objects, and the distribution of the $U$ objects is determined by their places in that string (or by the places of the $k-1$ separators); $(1)$ gives the number of ways to choose those places.

Answer 2

The expression $k+U-1\choose U$ counts the number of multisets of size $U$ drawn from $\{1,2,\dots,k\}$.

When $k=3$ and $U=2$, they are $\{1,1\}$, $\{1,2\}$, $\{1,3\}$, $\{2,2\}$, $\{2,3\}$, and $\{3,3\}$. These correspond to inserting the two unlabelled objects $U$ together with various separators. For example, $\{1,1\}$ corresponds to putting both $U$s with separator 1, while $\{1,2\}$ corresponds to putting one of the $U$s with separator 1 and the other one with separator 2. Each of these six multisets gives a "pattern" of 3 non-consecutive values in a circle of 8 unlabelled objects. Here are the six patterns, where a white dot is either a separator or one of the $U$s:

For each pattern, there are $n$ consistent ways to number the objects: put any value from 1 to $n$ at the top and add one (modulo $n$!) as you go around clockwise. The numbers in positions marked with $k$s (black dots in my picture) gives us a selection of $k$ non-consecutive values from $\{1,2,\dots,n\}$. As you run through all the patterns and all the numberings, each selection appears exactly $k$ times.

Therefore $\#\text{distinct selections}={n\over k}\times\#\text{patterns}.$