The limit as $n$ approaches infinity of $\, ^nz$ (the $n$ times iterated exponential or power tower function) converges for the bases
${\displaystyle \textstyle (e^{-1})^{e}\leq z\leq e^{e^{-1}}}, \tag*{}$
where
$\displaystyle e^{-e}=\frac{1}{e^e} \approx 0.0659880358453125 \tag*{}$
$\large e^{e^{-1}}= e^{ \frac{1}{e}} \approx 1.44466786100977 \tag*{}$
It can be verified that when the value of $z$ is between the two numerical values above, the infinite iterated exponential $\, ^{\infty }z$ or $z^{z^{z^{\cdots\infty}}}$ (determined by the relation involving the product log shown below) has a real valued numerical solution.
The infinite power tower or infinite tetration ${\displaystyle z^{z^{z^{\cdot ^{\cdot ^{\cdot }}}}}\!}$ can be extended to complex numbers or to the complex plane.
This infinite power tower has the general value
${\displaystyle h(z)={\frac {W(-\ln(z))}{-\ln(z)}}} \quad (1), \tag*{}$
where $\ln(z)$ is the principal branch of the complex logarithmic function, and $W(u)$ is the Lambert W function or the product log function, defined as:
${\displaystyle u = y e^y \Leftrightarrow y = W(u).} \tag*{}$
For additional clarification, here is the proof of the relation $(1)$ above:
Let
${\displaystyle z^{h}=h} \tag*{}$
Then
${\displaystyle z=h^{1/h}} \tag*{}$
${\displaystyle z^{-1}=h^{-1/h}} \tag*{}$
${\displaystyle {\frac {1}{z}}=\left({\frac {1}{h}}\right)^{1/h}} \tag*{}$
${\displaystyle -\ln(z)=\left({\frac {1}{h}}\right)\ln \left({\frac {1}{h}}\right)} \tag*{}$
${\displaystyle -\ln(z)=e^{\ln \left({\frac {1}{h}}\right)}\ln \left({\frac {1}{h}}\right)} \tag*{}$
${\displaystyle \ln \left({\frac {1}{h}}\right)=W(-\ln(z))} \tag*{}$
${\displaystyle {\frac {1}{h}}=e^{W(-\ln(z))}} \tag*{}$
${\displaystyle {\frac {1}{h}}={\frac {-\ln(z)}{W(-\ln(z))}}} \tag*{}$
${\displaystyle h={\frac {W(-\ln(z))}{-\ln(z)}}.} \tag*{}$
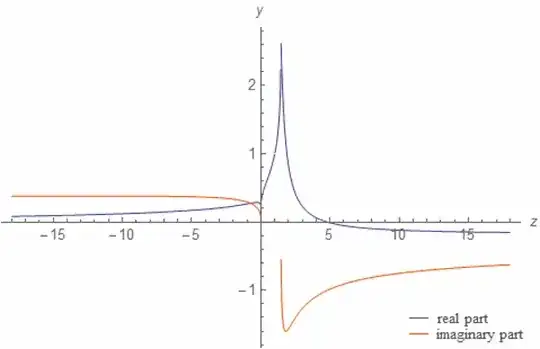
Below is a plot of $(1)$ (from wolfram Alpha):
For $z = 2$ we have the following result:
$\boxed{\displaystyle {2^{2^{2^{2 ...}}}= h(2) = -\frac{W(-\ln (2))}{\ln (2)}}=\frac{W_0(-\ln (2))}{\ln (2)}}, \tag*{}$
where $W_0$ is the main branch of the Lambert W function.
The numerical value of $h(2)$ is (verified with Mathematica):
$\displaystyle \begin{align}
2^{2^{2^{2 ...}}} &= h(2) \\ &\approx 0.8246785461420742223140645943816032399746074201816 \\ &\quad -1.5674321238496478610585743911929869275333075742042 i \end{align} \tag*{}$
Wolfram Alpha providess the following symbolic result :
$\displaystyle -\frac{W(-\ln (2))}{\ln (2)}= \frac{1}{\pi \ln(2)} \int_{-\infty }^{-\frac{1}{e}} \ln \left(\frac{x+\ln (2)}{x}\right) \Im\left(\frac{\partial W(x)}{\partial x}\right) \, dx ,\tag*{}$
where $\Im(z)$ is the imaginary part of $z$ .
The last result above can be numerically verified and approximated with Mathematica by typing :
NIntegrate[
Im[D[ProductLog[x], {x}]]*
Log[(x + Log[2])/x], {x, -Infinity, -(1/E)}]/(Pi*Log[2])
For another value such as $z = \sqrt{2},$ we get:
$\displaystyle \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{.^{.^.}}}} = h(\sqrt{2})= -\frac{W(-\ln (\sqrt{2}))}{\ln (\sqrt{2})}=2 \tag*{}$