Is the reverse of the first derivative test statement true?

Question

The first derivative test says that if the derivative of a function is positive/negative in the open interval $(x-a,x)$ and negative/positive in the open interval $(x,x+b)$ where both $a$ and $b$ are greater than zero, then there is a local maxima/minima at $x$. Is the reverse of this statement true ?

For example, if $x$ is a local maxima of the function $f(x)$ and if the function $f(x)$ is continuous and differentiable in $(a,b)$ where $a < x < b$, then there exists an interval to the left of $x$, howsoever small, in which the function has a positive slope and an interval to the right of $x$, howsoever small, in which the function has a negative slope.

Answer 1

TL;DR: The answer is no, and I provide a counterexample. See md2perpe’s comment on this answer for more details.

Consider the function:

$f(x) = x^2(\sin(1/x)-1.5)$ for $x \neq 0$ and $f(0) = 0.$

This is what the graph looks like (from WolframAlpha)

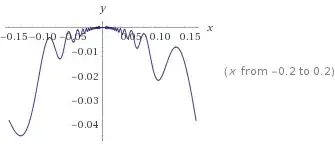$f(x) = x^2(\sin(1/x)-1.5)$ ">

$$$$ Then:

$f(x) < 0 $ for all $ x \neq 0$ because $ x^2 > 0 \ \forall x \neq 0 $ and $\sin(1/x)-1.5 < 0 \ \forall x \neq 0$. Hence the origin is a local (in fact, global) maximum.

Using the same method as the main answer to this question, we see that $f’(0) = 0.$

Furthermore, for $x \neq 0,\ f’(x) = 2x(\sin(1/x) - 1.5) - \cos(1/x),\ $ which is defined for all values $x \neq 0.$

Therefore $f’(x)$ is differentiable for all x in some interval containing the maximum (the origin). (In fact, we see that $f(x)$ is differentiable for all x).

However, we just found what the derivative of $f(x)$ is for $x \neq 0$: $f’(x) = 2x(\sin(1/x) - 1.5) - \cos(1/x)$, which, as $x {\to} 0,\ $ tends to $-\cos(1/x)$, and so oscillates between approximately -1 and 1 (as $x {\to} 0$).

If you want to know where my idea for this came from, I am somewhat familiar with the graph of $g(x) = x^2\sin(1/x)\ $ for $ x \neq 0 $ and $f(0) = 0.$

I considered “pushing the points” (other than the origin) downwards to just below $y=0$. I noted that $x^2\sin(1/x)$ just touches the graph of $ y=x^2$ at various points (as $x {\to} 0$), so I first considered $x^2\sin(1/x) - x^2,\ $ which, by the way, is the same as $x^2(\sin(1/x) - 1),\ $ and this would have been sufficient if the question didn’t require strict maximum. So for a strict maximum, I tried 1.5 instead of 1 and voila!.