How to understand this inequality intuitively?
$$\sqrt{a b} \leq \frac{a+b}{2}, \: a,b \ge 0$$
The right part is a number between $a$ and $b$. This is the only thing I have realised about this inequality.
Hope you guys some insight to share.
Kind regards,
Here you can see a geometric intuition based on the second Euclid Theorem 
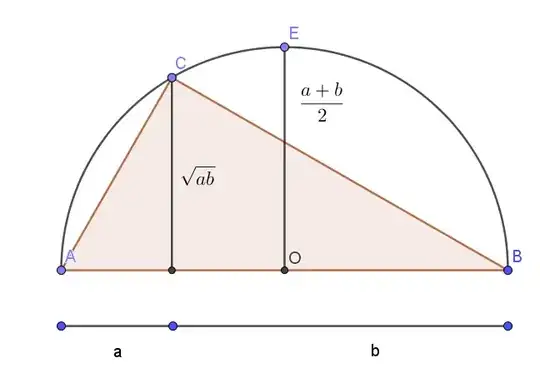
For the specific case of the AM-GM inequality with $n=2$, a nice way to see it is to identify $ab$ as the area of a rectangle with sides $a$ and $b$ and $\left ( \frac{a+b}{2} \right )^2$ as the area of a square with sides $(a+b)/2$. These have the same perimeter; the area of the square is bigger, unless $a=b$ in which case they were the same shape to begin with. The case $n=3$ has a similar picture with the volume of a rectangular prism with a fixed total edge length being biggest when the prism is a cube.
Besides that I'll make some algebra/calculus comments where I focus on the case $n=2$, but basically the same considerations extend to the general case.
Say $a \leq b$ for definiteness.
When $b=a$, the geometric and arithmetic means are the same. What happens as $b$ increases with $a$ fixed? Certainly in the $b \to \infty$ limit, the arithmetic mean grows much much faster, scaling linearly in $b$ instead of as $\sqrt{b}$.
Does this also happen down near $b=a$? Yes; for instance the derivative of $\sqrt{ab}$ with respect to $b$ is $\frac{1}{2} \sqrt{\frac{a}{b}} \leq 1/2$ with equality only when $b=a$. Meanwhile the derivative of $\frac{a+b}{2}$ with respect to $b$ is of course $1/2$ everywhere. Note that in this thinking, only the $b \to \infty$ case was really "obvious", but once we know what is happening there (and that it doesn't depend on what $a$ is), it is natural to do a little bit more calculation to determine whether there is a crossover or not.
In general the geometric mean is pulled down more by its smallest constituent than the arithmetic mean is, while the arithmetic mean is pulled up more by its largest constituent than the geometric mean is (assuming positive constituents in each case). To quantify that, say the smallest constituent is $\varepsilon$ and the other constituents multiply to $P$ and sum to $S$. Then as $\varepsilon \to 0$, the geometric mean is $(\varepsilon P)^{1/n}$ which goes to zero, while the arithmetic mean is $\frac{S+\varepsilon}{n}$ which doesn't go to zero. On the other hand if the largest constituent is $M$ and we introduce $P$ and $S$ in the same way, then the geometric mean grows as $(MP)^{1/n}$ but the arithmetic mean grows considerably faster, behaving as $\frac{M+S}{n}$.
If you know, that $(x-y)^2 = x^2 - 2xy + y^2 \geq 0$, then you can eazily prove it by writing it this way:
$$\frac{a+b-2\sqrt{ab}}{2} \geq0 \iff \frac{(a-b)^2}{2} \geq 0$$
Here we want to only explain why
$\quad \sqrt{a b} \lt \frac{a+b}{2}, \: a,b \gt 0 \text{ and } a \lt b$
since we have equalities when $a = b$ (the 'limiting' case).
We can write $a = u^2$ and $b = v^2$ with $0 \lt u \lt v$.
So now looking at (pondering)
$\tag 1 uv \lt \frac{u^2+v^2}{2} = \frac{u^2}{2} + \frac{v^2}{2}$
Now $uv$ represents the area of a rectangle, This rectangle in contained in a larger rectangle with area $v^2$. It also contains a smaller rectangle of area $u^2$.
Let $u$ be an even integer $n$ and $v = n + 1$. Divide up the 'master floor plan' rectangle of area $v^2$ into unit squares to 'see' why $\text{(1)}$ is true.
Here is the picture for $u =6$ and $v = 7$: After the 'easy part', there are $\frac{7}{2}$ unit squares on the bottom edge that can be used for the remaining $3$ unit squares on the top-right. So we have it!
The 'picture argument' made here works exactly the same for any general $0 \lt u \lt v$ configuration, where you 'paint' the $u \times v$ area using 'whole-chunk rectangular pieces'.
A simple algebraic proof using these ideas can be found here.
Graph the line $x+y=ab$ and the hyperbola $xy=ab$ the former intersects the line $y=x$ at coordinate $(x+y)/2$, the latter intersects ibstead st coordinate $\sqrt{ab}$. The hyperbola sags towards its center (the origin) before moving outwards along either asymptote, so $\sqrt{ab}<(a+b)/2$.
