Is there a geometry where the distance between two points can be complex?

Question

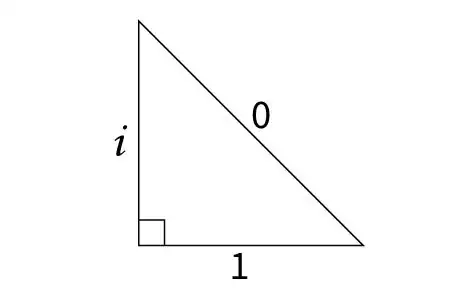
This tweet contained this image which is of course complete nonsense but it got me thinking -- is there such a thing where the distance of two points is a complex number?

Ps. it seems such questions are fit for this SE for example Can there be a geometry where angles can be infinite?

If by "distance" you mean metric, then no: a metric is by definition real valued — G. Chiusole, Apr 05 '20 at 18:06

chx · Answer 1 · 2020-04-05T19:52:35.467

5

Akbar Azam, Brian Fisher & M. Khan (2011) Common Fixed Point Theorems in Complex Valued Metric Spaces, Numerical Functional Analysis and Optimization, 32:3, 243-253, DOI: 10.1080/01630563.2011.533046

We introduce complex valued metric spaces and obtain sufficient conditions for the existence of common fixed points of a pair of mappings satisfying contractive type conditions.

While I can't find this paper freely available online, this PDF cites it and defines " XxX→C is called a complex valued b-metric":

edited Apr 05 '20 at 19:52

answered Apr 05 '20 at 18:10

chx

1,807

Fair enough, I deleted my comment. That's the trouble with words, you get these "eats shoots and leaves" problems. – Guy Inchbald Apr 05 '20 at 20:04

score 1 · Answer 2 · answered Apr 05 '20 at 18:06

1

There can be no such metric, as it would not obey the requirements of a metric. Specifically, you must be able to have the "$>$" operation (for the triangle inequality: $d(a,b) + d(b,c) \geq d(a,c)$), and that does not hold for complex numbers.

answered Apr 05 '20 at 18:06

David G. Stork

29,774

-1: the question doesn't even contain the word "metric". And you could apply your answer to the word "measure", yet complex and even operator-valued measures are a thing (and a useful one!). – Martin Argerami Apr 06 '20 at 04:06
@MartinArgerami: "distance" implies the metric, for instance "Euclidean distance" is a direct result of a "Euclidean metric." Any distance must obey the rules of a metric: $d(x,x) = 0$, $d(x,y) = d(y,x)$, and $d(x,y) + d(y,z) \geq d(x,z)$. Look it up. – David G. Stork Apr 06 '20 at 04:51
@MartinArgerami is there a complex valued measure on the one dimensional Euclidean space ? – chx Apr 06 '20 at 06:04
Yes, lots.$\ \ $ – Martin Argerami Apr 06 '20 at 06:43

score 1 · Answer 3 · answered Apr 05 '20 at 18:25

A distance is always a real number, for reasons given in other answers. It is only when the angle is also introduced to make it a vector that things get complex. For example the shortest distance from one point to another is a real number, but the shortest path is a vector and may prove to be complex.

Is there a geometry where the distance between two points can be complex?

3 Answers3