Formula with 2 points of inflection

Question

$x^3$ has a point of inflection at $x=0$. How will you modify the formula to add a 2nd point of inflection at $x=1$?

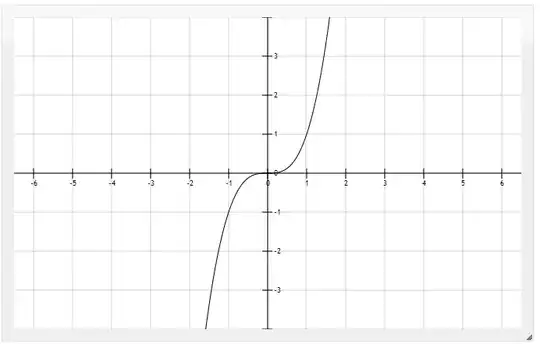
Plot of $x^3$ enter image description here

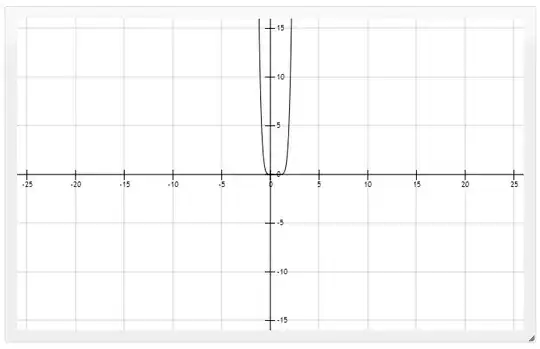
Plot of $x^3(x-1)^3$ enter image description here

Update

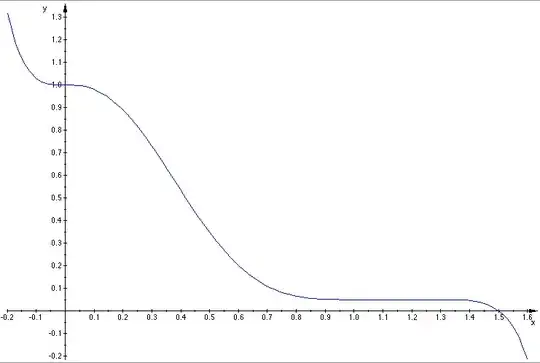
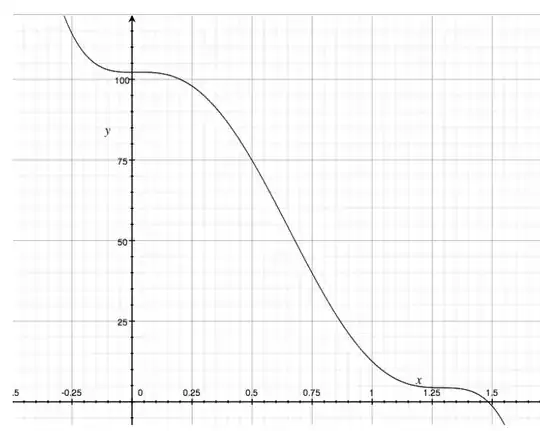
The plot I am aiming to achieve has a shape similar to the graph below. However I would like the 2 inflection points at $(0, 1)$ and $(1, 0.05)$, and intersects the x-axis at $(1.5,0)$ and y-axis at $(0,1)$.

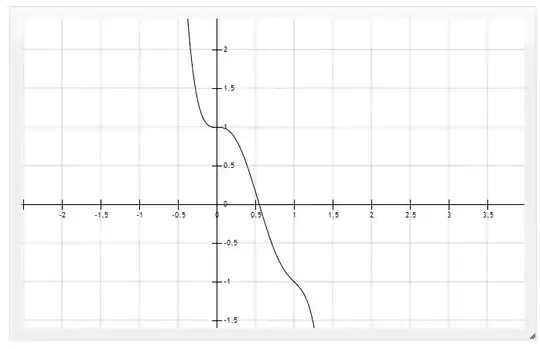
Graph with similar target shape enter image description here

Current attempt

The closest I can get is using $1 - [ 16x^3 - 23x^4 + 9x^5 ]$ using J.M.'s equation inside the $[]$ square brackets with $\alpha=2$ and $\beta=1$. How should I bring the point of inflection at $x=1$ up to around $y=0.05$? Its currently at $y=-1$

enter image description here

But your second diagram seems to have a point of inflection at $x=1.25$, not $x=1$. — TonyK, Apr 13 '13 at 20:18
I just saw your update. Are you trying to get the equation of the second graph? Meaning two inflections points at $(0,105)$ and $(1.25,5)$? Or just any equation with two inflections, one along $x = 0$ and another along $x = 1$? — Jerry, Apr 13 '13 at 20:19
@TonyK I would like a point of inflection at 1 instead. Will it be easy to adjust the point of inflection between $x=1$ to $x=1.25$? — Nyxynyx, Apr 13 '13 at 20:27
@Jerry Sorry for the confusion, I've updated the question to make it clearer. I'm looking to get inflection points $(0, 1)$ and $(1, 0.05)$, and intersects the x-axis at $(1.5,0)$ and y-axis at $(0,1)$ — Nyxynyx, Apr 13 '13 at 20:32
@Nyxynyx: Notthing wrong with the software. From the wording, I assumed you wanted a point of inflection at $0$ and $1$ (and possibly at other points), hence the suggestion $x^3(x-1)^3$. — André Nicolas, Apr 13 '13 at 22:03
@Nyxynyx: to be honest my answer was merely a repetition of J.M.'s answer hours earlier (as I just noticed). Choosing his answer instead of mine would be fine or better ! — Raymond Manzoni, Apr 14 '13 at 17:48

J. M. ain't a mathematician · Answer 1 · 2013-04-14T11:10:35.030

2

One rather general family is given by

$$2(5\alpha-2\beta)x^3+(7\beta-15\alpha)x^4+3(2\alpha-\beta)x^5$$

I obtained this through Hermite interpolation. That involves derivatives, so I'm not sure if this counts for a "precalculus" answer.

I would like the 2 inflection points at $(0,1)$ and $(1,0.05)$, and intersects the x-axis at $(1.5,0)$ and y-axis at $(0,1)$.

Using Hermite interpolation again, we obtain the polynomial

$$1-\frac{3977}{270}x^3+\frac{5389}{180}x^4-\frac{385}{18}x^5+\frac{706}{135}x^6$$

You can easily verify that this has the properties needed.

Another possibility, whose shape is a bit nearer to what the OP seems to want, is

$$1-\frac{6491}{270}x^3+\frac{34603}{540}x^4-\frac{1223}{18}x^5+\frac{4477}{135}x^6-\frac{838}{135}x^7$$

edited Apr 14 '13 at 11:10

answered Apr 13 '13 at 19:44

J. M. ain't a mathematician

75,051

Thank you, that does get me a second point of inflection. Updated my question with the target plot I aim to get, any suggestions on how I can move the y position of the inflection point at x=1 higher? – Nyxynyx Apr 13 '13 at 20:10
That's what the adjustable parameters are for. Try evaluating the general polynomial at $x=1$ and see what happens. – J. M. ain't a mathematician Apr 14 '13 at 01:22
Oups it's only now that I observe that I merely repeated your answer (no your two answers!!). Sorry... (you got my vote anyway). – Raymond Manzoni Apr 14 '13 at 17:40

Raymond Manzoni · Accepted Answer · 2013-04-14T17:27:22.700

2

It seems that there is an implicit constraint (because else George V. Williams' answer (+1) would be perfect !) : that the derivatives at $x=0$ and $1$ are $0$ !

With these constraints I got a polynomial of degree $6$ $P(x)=\frac{706}{135}x^6-\frac{385}{18}x^5+\frac{5389}{180}x^4-\frac{3977}{270}x^3+1$
but the behavior was not nice near $\frac 32$ so that I tried again with a polynomial of degree $7$ and the additional constraint $P'\left(\frac 32\right)=-1$ (change this if wished !) : $$P(x)=a x^7+b x^6+c x^5+dx^4+ex^3+fx^2+gx+h$$ From $P(0)=1$ we get $\ h=1$
From $P(1)=\frac 1{20}$ we get $\ a+b+c+d+e+f+g=\frac 1{20}-1$
We want too $P\left(\frac 32\right)=0$ but will write this down later...
$$P'(x)=7ax^6+6b x^5+5c x^4+4dx^3+3ex^2+2fx+g$$ Should $P'(0)=P'(1)=0$ be wished then $g=0\ $ and $\ 7a+6b+5c+4d+3e+2f=0$
(we will impose too $P'\left(\frac 32\right)=-1$ at the end) $$P''(x)=42ax^5+30b x^4+20c x^3+12dx^2+6ex+2f$$

From $P''(0)=P''(1)=0$ we get $f=0\ $ and $\ 7a+5b+\frac {10}3c+2d+e=0$

Let's put everything together (the two last lines from the array concern $64P'\left(\frac 32\right)$ and $128P\left(\frac 32\right)$) : $$P(x)=a x^7+bx^6+c x^5+dx^4+ex^3+1$$ with \begin{array}{cccccc} a &+b &+c &+d &+e&= &-\frac{19}{20}\\ 7a &+6b &+5c &+4d &+3e &= &0\\ 7a &+5b &+\frac {10}3c&+2d&+e&=&0\\ 5103a &+ 2916b &+ 1620c &+ 864d &+ 432e &=&-64\\ 2187a &+ 1458 b &+ 972 c &+ 648d &+ 432e &=&-128\\ \end{array}

The solution deduced from this system is : $$P(x)=-\frac{838}{135}x^7+\frac{4477}{135}x^6-\frac{1223}{18}x^5+\frac{34603}{540}x^4-\frac{6491}{270}x^3+1$$

with the picture : polynomial of degree 7

edited Apr 14 '13 at 17:27

answered Apr 14 '13 at 15:49

Raymond Manzoni

43,021
5
86
140

No surprise that we obtained the same polynomial... Hermite interpolation is pretty powerful. :) – J. M. ain't a mathematician Apr 14 '13 at 17:38
@J.M. : I just noticed that and was commenting on your answer while you commented here :-) – Raymond Manzoni Apr 14 '13 at 17:41
It's just as well that you explicitly demonstrated how one constructs a Hermite interpolant. (I upvoted your answer, of course. :)) – J. M. ain't a mathematician Apr 14 '13 at 17:50
@J.M. and you even got the $-1$ tangent at $\frac 32$ I selected... (looks suspicious now ;-)). I thought that your method was merely a higher degree polynomial approximation (it seems I was pretty wrong...) – Raymond Manzoni Apr 14 '13 at 17:55
"...you even got the $−1$ tangent at $\frac32$ I selected" - I was lazy and wanted to ease the algebra a bit by picking a convenient slope. :D That we thought alike isn't a bad thing, I think. – J. M. ain't a mathematician Apr 14 '13 at 18:01
@J.M. It is at least the second 'follow-through'. Your style is shorter ! :-) – Raymond Manzoni Apr 14 '13 at 18:07

score 1 · Answer 3 · answered Apr 13 '13 at 20:59

Use a fourth-degree polynomial $f(x) = ax^4 + bx^3 + cx^2 + dx + e$, and get that:

$$ f''(x) = 12ax^2 + 6bx + c = 0 \text{ at } x = 0 \text{ and } 1$$

So we get that:

$$ c = 0 \text{ and } 12a + 6b = 0$$

Well that's still not enough! Based on what you said, we also know that $e = 1$ (since $f(0) = 1$). We also need that:

$$f(1) = a+b+c+d+e = \\ a + b + d + 1 = 0.05$$

So close, and your last criterion, that $f(1.5) = 0$, will let us finish it:

$$ 5.0625 a + 3.375 b + 1.5d + 1 = 0$$

We have the following system of equations:

$$ 2a + b = 0 \\ a + b + d + 1 = 0.05 \\ 5.0625 a + 3.375 b + 1.5d + 1 = 0 $$

Solving the system of equations, we get:

$$a = -\frac{34}{15} \\ b = \frac{68}{15} \\ d = -\frac{193}{60} $$

Graphing the result:

image graph

score 0 · Answer 4 · answered Apr 13 '13 at 20:23

A fourth degree polynomial can have two points of inflection. Let's pick an arbitrary one: $f(x) = ax^4 + bx^3 + cx^2 + dx + e$.

Inflection points occur when the second derivative is $0$: $f^{\prime\prime}(x) = 12ax^2 + 6bx^2 + c = 0$. We want these roots to occur at 0 and 1.

Substituting $x=0$, we get $c = 0$. Substituting $x=1$, we can pick $a = 1, b = -2$. Put these back into the original equation: $x^4 - 2x^3 + dx + e$. One solution is simply $x^4 - 2x^3$, but a prettier one is $x^4 - 2x^3 + x + \frac{1}{4}$

Formula with 2 points of inflection

Update

4 Answers4