1

I have an optimization problem in the form of:

$\min_x \quad u^Tx \\ s.t. \quad (x-\textbf{1/2})^2 - \vert x-\textbf{1/2}\vert \leq \textbf{-1/4}$.

Since the constrained of this problem is not convex, the standard convex programming methods cannot be applied. I learned that DC (difference of convex) programming and convex-concave programming (CCCP) can be used to solve this problem. However, I did understand their differences, or their capability to provide an algorithm (e.g., DCA) to converge to the global optimal solution.

Just to recap, I have two questions:

  1. What are the differences of CCCP and DC programming, especially in terms of their convergence to the global optimal solution?

  2. Are they convergent to the global optimal solution?!

Any help is appreciated!

Edit:

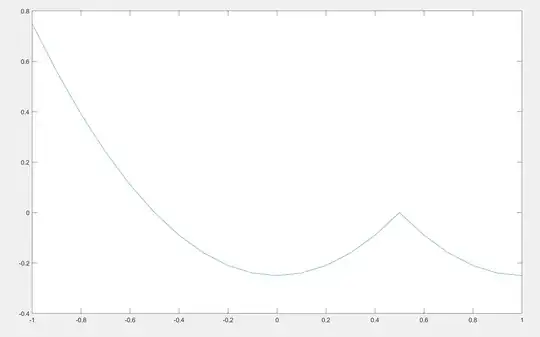
The shape of the constraint function is as below:

enter image description here

Zenan Li
  • 1,404
Majid Mohammadi
  • 99
  • What do you mean by the square of a vector in the constraint? Is this a pointwise inequality, or is $|\cdot|$ some norm? – Michal Adamaszek Mar 31 '20 at 14:01
  • @MichalAdamaszek Yes, both power and absolute value are element-wise operations. – Majid Mohammadi Apr 01 '20 at 15:04
  • But $|t|\geq t^2$ for $t\in\mathbb{R}$ is equivalent to $t\in[-1,1]$, so I don't understand the non-convexity issue. – Michal Adamaszek Apr 01 '20 at 15:15
  • I plotted the function, it is not convex but bi-modal. – Majid Mohammadi Apr 01 '20 at 19:11
  • OK, but now you changed the constraint :). There used to be 0 on the RHS :). – Michal Adamaszek Apr 01 '20 at 19:21
  • I edited the post to basically add the figure, but not successful the first time. Whatever is on the RHS, that does not make any difference. The function is not convex. I added the figure now! – Majid Mohammadi Apr 02 '20 at 08:59
  • The RHS makes a lot of difference, because the function is not convex, but the constraint can still describe a convex set (and for RHS>=0 it does). Anyhow, you should be able to implement it as a mixed-integer quadratic or second order cone program, choosing binary variables to describe which part of the graph you are in. – Michal Adamaszek Apr 02 '20 at 11:58
  • Also, you may get better answers if you write the full problem you want to solve, no just the one constraint. – Michal Adamaszek Apr 02 '20 at 12:03
  • @MichalAdamaszek Thanks for the reply Michal! The other constraint is a linear inequality constraint that I guess would not impose any problem! But about the non-convexity, I still believe that the function is not convex, no matter what RHS we have. Any RHS would only move up/down the figure, and has no influence on the convexity. – Majid Mohammadi Apr 03 '20 at 12:06
  • Once more, you confuse the notions. The function $f(x)$ in your constraint is not convex, but the set ${x:f(x)<10}$ is convex. I understand that you can't exploit it because you have $f(x)<-0.25$ instead, however, in principle, for some values of the bound your problem is convex and easy and for others it is not. – Michal Adamaszek Apr 03 '20 at 12:44

1 Answers1

1

I am not sure whether I misunderstand OP's problem. To solve this problem, why not Dividing the constraint into two parts such that it becomes two convex optimization problems: \begin{equation} \begin{array}{cl} {\min} & {u^T x} \\ {\text{s.t.}} & {(x-\frac{1}{2})^2+(x-\frac{1}{2}) \leq -\frac{1}{4}} \\ {} & {x \leq \frac{1}{2}} \end{array} \end{equation} and \begin{equation} \begin{array}{cl} {\min} & {u^T x} \\ {\text{s.t.}} & {(x-\frac{1}{2})^2-(x-\frac{1}{2}) \leq -\frac{1}{4}} \\ {} & {x \ge \frac{1}{2}} \end{array} \end{equation} Then solve these two convex optimization problem at the same time, and the optimal solution of original problem is the lower objective value.

For DC programming and CCCP, in my humble opinion, I think these two method is the same method, although the first one analyze the problem in dual perspective and the second one describe the method in a more friendly way. In addition, the author of DC programming discusses some more DC decomposition methods.

And both DC programming and CCCP could not converge to global optimal solution. They are both convergent globally, that means they can converge for any initial point.

Zenan Li
  • 1,404
  • Thanks for the answer. Please keep in mind that x in a multi-dimensional vector. So I guess, if taken your approach, we need to assume that each variable is either >1/2 or <1/2, and that makes 2^n problems, where n is the size of x (as far as I could understand from your answer). If it is the case, then it is not efficient at all. – Majid Mohammadi Apr 03 '20 at 12:13
  • 1
    @MajidMohammadi If you implement it with integer variables as a mixed-integer problem the solver will cut off some branches. I would try that approach. – Michal Adamaszek Apr 03 '20 at 12:42
  • @MajidMohammadi So how many constraints in your problem? if the size of $x$ is $n$, the number of constraints is also $n$, right? Or in other words, is it a vector constraints in your problem? Could I rewrite these constraints into $(x_i-\frac{1}{2})^2 + |x_i - \frac{1}{2}| \leq - \frac{1}{4}$ for each component of $x$? – Zenan Li Apr 03 '20 at 15:04
  • @MajidMohammadi I know your consideration, but if the constraint is independent for each component of $x$, we can solve them respectively. – Zenan Li Apr 03 '20 at 15:13
  • Yes the constraint is element-wise, so basically we have n constraints. The constraints are independent indeed, but we need to consider all the constraints for solving the problem. – Majid Mohammadi Apr 03 '20 at 17:18
  • @MajidMohammadi Since the constraint is element-wise, and the objective function is linear, so we can solve them independently, i.e., $\min_{x_i} u_i x_i, \quad \text{s.t.}~ (x_i-\frac{1}{2})^2+|x_i-\frac{1}{2}| \leq - \frac{1}{4}$, right? – Zenan Li Apr 03 '20 at 23:33
  • Then just compute the summation of optimal value of these $n$ subproblems. – Zenan Li Apr 03 '20 at 23:34