For $n\ge 1$, define $a_n=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}-\log n$. Prove that $\lim_{n\to\infty} a_n$ exists.

Question

Question: For $n\ge 1$, define $a_n=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}-\log n$. Prove that $\lim_{n\to\infty} a_n$ exists.

My approach: For any $n\in\mathbb{N},$ $$a_{n}-a_{n+1}=-\frac{1}{n+1}-\ln n+\ln(n+1)\\ =\ln\left(1+\frac{1}{n}\right)-\frac{1}{n+1}.$$

Now we have $$\frac{1}{n+1}<\ln\left(1+\frac{1}{n}\right)<\frac{1}{n}, \forall n\in\mathbb{N}.$$

Therefore, $$\ln\left(1+\frac{1}{n}\right)-\frac{1}{n+1}>0\\ \implies a_{n}-a_{n+1}>0 \\ \implies a_{n}>a_{n+1}, \forall n\in\mathbb{N}.$$

This implies that the sequence $\{a_n\}_{n\ge 1}$ is strictly monotonically decreasing.

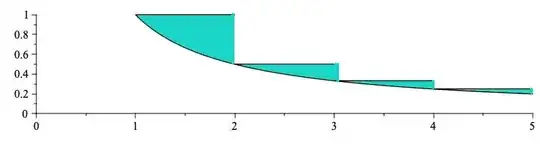
Now let us take any $n\in\mathbb{N}$ and approximate the area under the curve $f(x)=\frac{1}{x}, x>0$ represented by the interval $[1,n+1]$.

Now using definite integral we can approximate the area to be $$A_n=\int_1^{n+1}\frac{dx}{x}=\ln(n+1).$$

Now let us approximate the area using the rectangle method and call that area to be $S_n$.

To do the same, let us divide the interval into $n$ equal parts in order to have each interval having length $1$. Thus the $n$ intervals will be $[1,2],[2,3],\cdots, [n,n+1].$ Also, we would need to define a function $g:[1,\infty)\to \mathbb{R}$, such that $$g(x)=\frac{1}{[x]}, \forall x.$$

Therefore, $$S_n=f(1).1+f(2).1+f(3).1+\cdots+f(n).1\\ =g(1).1+g(2).1+g(3).1+\cdots+g(n).1 \\=\left(\frac{1}{1}\right)1+\left(\frac{1}{2}\right)1+\cdots+\left(\frac{1}{n}\right)1\\=\sum_{i=1}^n\frac{1}{i}.$$

Now since $\forall x\ge 1,$ $$[x]\le x\\ \implies \frac{1}{[x]}\ge \frac{1}{x}([x]=x,\text{ holds true only at integer points, hence }\frac{1}{[x]}=\frac{1}{x},\text{ holds true only at integer points})\\ \implies S_n>A_n\\ \implies \sum_{i=1}^n\frac{1}{i}>\ln(n+1).$$

Therefore, we have $$\sum_{i=1}^n\frac{1}{i}>\ln(n+1)>\ln n\\ \implies\sum_{i=1}^n\frac{1}{i}>\ln n\\ \implies \sum_{i=1}^n\frac{1}{i}-\ln n>0 \\ \implies a_n>0, \forall n\in\mathbb{N}.$$

Therefore, the sequence $\{a_n\}_{n\ge 1}$ is monotonically decreasing and bounded below, hence it is convergent, that is $\lim_{n\to\infty}a_n$ exists and is finite.

Is the solution correct and rigorous enough, and does there exist any alternate solution to this problem?

You can find it here https://en.wikipedia.org/wiki/Euler%E2%80%93Mascheroni_constant — maths, Mar 30 '20 at 10:45
This seems very close to Showing that $\lim_{n\to\infty}\sum^n_{k=1}\frac{1}{k}-\ln(n)=0.5772\ldots$ — robjohn, Mar 30 '20 at 10:54
This sequences converges to the Euler–Mascheroni constant. It’s very important in number theory. — maths, Mar 30 '20 at 10:42
@OlivierRoche: No, it is not correct. The OP says, for instance, "$\lim_{n\to\infty}\sum_{i=1}^n\frac{1}{i}$ exists". This is not true. — TonyK, Mar 30 '20 at 11:34
@OlivierRoche, yes the second part of the solution is terribly wrong! — Sanket Biswas, Mar 30 '20 at 11:43
@TonyK Indeed, I missed that part! So, to get everything in order, OP needs to rewrite the proof that $a_n > 0$ . — Olivier Roche, Mar 30 '20 at 11:47
I have edited the proof. Can someone check if it is now correct or not. — Sanket Biswas, Mar 30 '20 at 12:39

GEdgar · Answer 1 · 2020-03-30T20:17:01.217

Here is a pictorial answer. Some people may like it more than a wordy answer.

Let $$ A_n = \sum_{k=1}^{n-1}\frac{1}{k} - \log n $$ Since $A_n$ differs from the term in the question by $\frac{1}{n}$ and $\frac{1}{n} \to 0$, it suffices to show that $A_n$ converges.

Here we have shaded something with area $A_5$.

The lower graph is $y=1/x$ between $x=1$ and $x=5$.
The horizontal line segments are:
$y=1$ from $x=1$ to $x=2$;
$y=1/2$ from $x=2$ to $x=3$;
$y=1/3$ from $x=3$ to $x=4$;
$y=1/4$ from $x=4$ to $x=5$.
The area beow the graph of $y=1/x$ is $\int_1^5\frac{dx}{x} = \log 5$. The area below the horizontal line segments is $\sum_{k=1}^4\frac{1}{k}$. The shaded area is the difference $A_5$.

Now translate these pieces to the left until they bump the $y$-axis.

The pieces are disjoint, and are contained in the square $[0,1] \times [0,1]$. When we go from $A_n$ to $A_{n+1}$ we add one more of these pieces. So the sequence $A_n$ is increasing, and bounded above by $1$. Therefore $A_n$ converges.

Olivier Roche · Accepted Answer · 2020-03-30T12:17:18.027

2

Your proof that $a_n>0, \forall n\in\mathbb{N}$ would be correct, except for this line, which you luckily don't use anyway:

This is false : $\lim_{n\to\infty}\sum_{i=1}^n\frac{1}{i}$ exists (no!) and is equal to $\int_1^{n+1}\frac{dx}{x}=\ln(n+1).$

What you probably meant is "$\sum_{i=1}^n \frac{1}{i} > \ln n$ for all $n\in\mathbb{N}$", let's prove that :

First, notice that $$\ln(n) < \ln (n + 1) = \int_1^{n + 1} \frac{1}{x} dx$$

On the other hand, consider the step function $f : x \mapsto \frac{1}{\lfloor x \rfloor}$ , one has $$\sum_{i=1}^n \frac{1}{i} = \int_1^{n + 1} f(x) dx$$

The rest is left to the reader :)

edited Mar 30 '20 at 12:17

answered Mar 30 '20 at 12:00

Olivier Roche

5,319
9
16

Please you do not prove it. I am trying to prove it myself. – Sanket Biswas Mar 30 '20 at 12:04
@SanketBiswas alright, show us the proof :) – Olivier Roche Mar 30 '20 at 12:17
I have edited the solution. Please check if it is correct or not. – Sanket Biswas Mar 30 '20 at 12:38
@SanketBiswas You need to introduce the definition of $A_n$ prior to referring to it. The most important argument misses : you get $A_n < S_n$ because for all $x > 1$, $f(x) < \frac{1}{x}$ (with my notations). – Olivier Roche Mar 30 '20 at 13:27
Please check if it is now correct or not. – Sanket Biswas Mar 30 '20 at 14:16
It seems correct, yes. Instead of that $\implies$ symbol, you should use short expressions in natural language, eg "Clearly, $\lfloor x \rfloor \leqslant x$ for $x\geqslant 1$, hence $\frac{1}{\lfloor x \rfloor} \geqslant \frac{1}{x}$ for $x\geqslant 1$. That's easier to read imho. – Olivier Roche Mar 30 '20 at 18:22
Oh and please upvote and/or accept an answer if it was helpful. ;) – Olivier Roche Mar 30 '20 at 18:34

score 1 · Answer 3 · answered Mar 30 '20 at 11:16

1

You wrote: $\lim_{n\to\infty}\sum_{i=1}^n\frac{1}{i}\text{ exists and is equal to }\int_1^{n+1}\frac{dx}{x}=\ln(n+1).$ But that sum is the famously divergent harmonic series. And also because of that, $S_n$ will not be larger than $\lim_{n\to\infty}\sum_{i=1}^n\frac{1}{i}$.

By comparing the areas (or integral test), $a_n\gt \log(n+1)-\log(n)$ is bounded below. And you have proved $\{a_n\}$ is monotonically decreasing, so that completes the proof.

answered Mar 30 '20 at 11:16

Divide1918

2,093

"$S_n$ will not be larger than $\lim_{n\to\infty}\sum_{i=1}^n\frac{1}{i}$": but this limit is $\infty$. Are you saying that $S_n$ will not be larger than $\infty$, or is there a misprint somwehere? – TonyK Mar 30 '20 at 11:21
That's kinda what I'm trying to say, except it's probably not a good idea to phrase it that way. – Divide1918 Mar 30 '20 at 11:24
@Divide1918, yes you are very right that $\sum_{i=1}^n\frac{1}{i}$ is basically the harmonic series and it diverges. Thanks for pointing out my mistake. – Sanket Biswas Mar 30 '20 at 11:33

score 1 · Answer 4 · answered Mar 30 '20 at 12:35

To answer OP's question of whether there is an alternate solution, the most expedite one is to Taylor expand \begin{align*} a_{n+1} - a_n & = - \ln \left ( 1 + \frac1n \right ) + \frac{1}{n+1} \\ & = - \frac1n + O \left ( \frac{1}{n^2} \right ) + \frac{1}{n+1} \\ & = - \frac{1}{n(n+1)} + O \left ( \frac{1}{n^2} \right ) \\ & = O \left ( \frac{1}{n^2} \right ). \end{align*} Therefore, the series $\sum(a_{n+1}-a_n)$ converges absolutely, and since it is a telescopic series, it means that $(a_n)$ converges.

For $n\ge 1$, define $a_n=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}-\log n$. Prove that $\lim_{n\to\infty} a_n$ exists.

4 Answers4

Linked