Apollonius fundamental properties of conic sections

Question

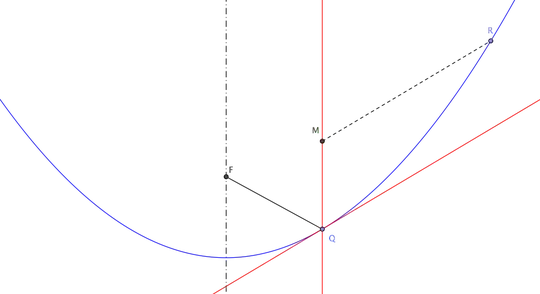
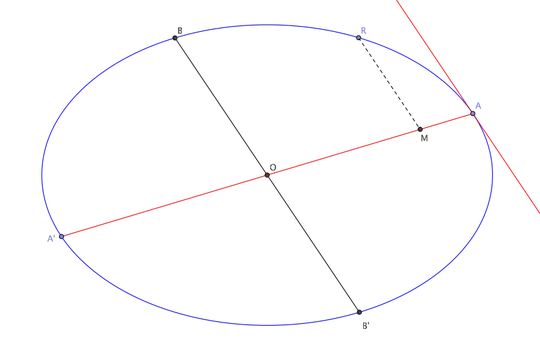
I am reading an old book which mentions the fundamental properties of conic sections in this way:

It was pointed out that the application of areas, as set forth in the second Book of Euclid and extended in the sixth, was made by Apollonius the means of expressing what he takes as the fundamental properties of the conic sections, namely the properties which we express by the Cartesian equations $$y^2 = px$$ $$y^2 = px \mp{p\over d}x^2$$ reffered to any diameter and the tangent at its extremity as axes...

I am trying to understand what these equations represent. Tried searching online to no success, I guess it is because the language was different back then. Does anyone know what is meant by this?

Read propositions 1 to 3 here: https://archive.org/details/treatiseonconics00apolrich/page/8/mode/2up — Intelligenti pauca, Mar 30 '20 at 22:19

Intelligenti pauca · Accepted Answer · 2020-04-02T20:02:20.680

1

In the case of a parabola, for instance, a diameter is any line parallel to the axis, as $QM$ in figure below. This line, and the line tangent at $Q$ to the parabola, can be taken as oblique coordinate axes: if $R$ is any point on the parabola, $y=RM$ and $x=QM$, then one can show that $$ y^2=px, $$ where line $RM$ is parallel to the tangent and $p=4QF$, point $F$ being the focus of the parabola. This is proven in Apollonius [I.49] (but Apollonius defines $p$ in a different equivalent way).

In the case of an ellipse, a diameter $AA'$ (i.e. a chord through the centre of the ellipse, see figure below) and the tangent at $A$ can be taken as oblique coordinate axes: if $R$ is any point on the ellipse, $x=AM$ and $y=RM$, then one can show that $$ y^2=px-{p\over d}x^2, $$ where line $RM$ and diameter $BB'$ are parallel to the tangent, $p=2{OB^2\over OA}$, $d=AA'$. This is proven in Apollonius [I.50], where the analogous statement is also proven for a hyperbola.

edited Apr 02 '20 at 20:02

answered Mar 31 '20 at 16:30

Intelligenti pauca

50,470
4
42
77

What does it mean "can be taken as oblique cartesian axes"? – Michael Munta Apr 02 '20 at 19:11
@MichaelMunta See here: https://mathworld.wolfram.com/ObliqueCoordinates.html – Intelligenti pauca Apr 02 '20 at 19:58
My use of the word "cartesian" here can be confusing: I'll change that. – Intelligenti pauca Apr 02 '20 at 20:01
So in the sentence "refered to any diameter and the tangent at its extremity as axes" the axes are these oblique coordinates? – Michael Munta Apr 02 '20 at 20:10
Yes, the oblique axes are a diameter and the tangent at one of its endpoints. – Intelligenti pauca Apr 02 '20 at 20:11
And what is the point of looking at them as axes? What do we achieve with that fact? – Michael Munta Apr 03 '20 at 06:23
@MichaelMunta It's a property that can be useful, I used it, for instance, in this answer. – Intelligenti pauca Apr 03 '20 at 14:13

Apollonius fundamental properties of conic sections

1 Answers1