0

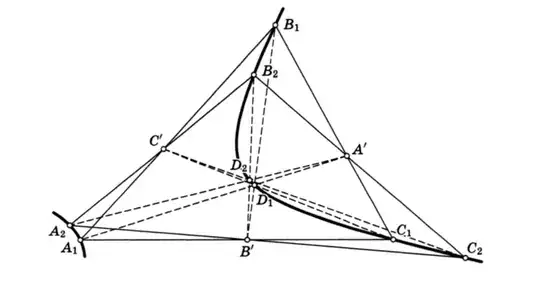
Suppose we are given two triangles $A_1B_1C_1$ ans $A_2B_2C_2$ and let $A'= B_1C_1 \cap B_2C_2, \: B'=C_1A_1 \cap C_2A_2, \: C'= A_1B_1 \cap A_2B_2$. Suppose that the triangle $A'B'C'$ is in perspective with the triangle $A_1B_1C_1$ as well as with $A_2B_2C_2$ from the centers of perspective (or perspectors) $D_1$ and $D_2$ respectively.

$\textbf{Problem}$: Show that the points $A_1, B_1, C_1, D_1, A_2, B_2, C_2, D_2$ lie on a conic.

I don't know what projective transformation or what theorem I could use to act in an appropriate way on those points. Many thanks for any suggestions or hints.

enter image description here

beginarray
  • 475

1 Answers1

0

The assertion is proved in Lemma 4.9 of Akopyan and Zaslavsky's Geometry of Conics:

Given four points (no three collinear) and their targets, there is a unique projective transformation that takes the points to their targets. So we can find a projective transformation that takes the quadrilateral $A_1B_1C_1D_1$ to a square. Since the points $A'$ and $C'$ are mapped to infinity in perpendicular directions, the quadrilateral $A_2B_2C_2D_2$ will become a rectangle whose sides are parallel to the sides of the square. Moreover, the image of the point $B'$ will be the center of both the square and the rectangle. Clearly, the conic passing through the vertices of the square and one of the vertices of the rectangle also passes through the other three vertices.

There is another (more analytic) proof in C. Bradley, Two Triangles and an Eight Point Conic

brainjam
  • 8,626