For $\triangle ABC$ with circumradius $R$, orthocenter $H$, and nine-point center $O_9$, show $O_9A^2+O_9B^2+O_9C^2+O_9H^2=3R^2$.

Question

Prove that, if $O_9$ is the nine-point center of triangle $ABC$ with $H$ as its orthocenter, then $$O_9A^2+O_9B^2+O_9C^2+O_9H^2=3R^2\,.$$

What I tried to do draw $O$ as $O_9$ is the midpoint of $OH$ and tried stuff as $AO=BO=CO=R$.

Answer 1

Let $\Delta ABC$ be a triangle with centroid $G$, then for any point $P$ we have the relation $$ \underbrace{PA^2 + PB^2 + PC^2}_{\sum PA^2} - 3PG^2 = GA^2 + GB^2 + GC^2 \ . $$ We write this relation for $O$ and $O_9$, thus getting $$ \sum O_9A^2-3O_9G^2 = \sum OA^2-3OG^2 = 3R^2-3OG^2\ . $$ Now note that the points $H,G,O,O_9$ are placed on the Euler line as follows: 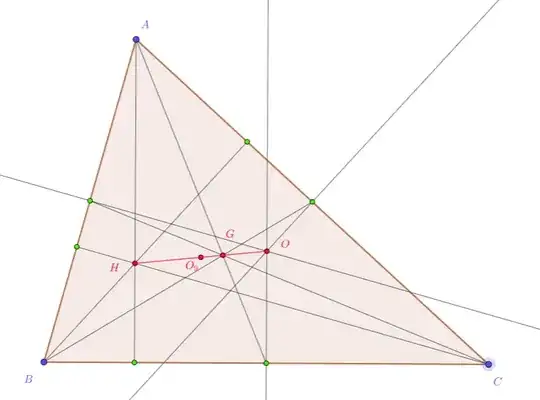Explicitly $O_9$ is the mid point of the segment $OH$, (since the projection of $O_9$ on each side is the mid point of the projected segment, which is a chord in the Euler circle), $G$ is placed in the proportion $GH:GO=2:1$ (same side projection argument), so $O_9G=\frac 13 O_9O=\frac 13 O_9H$. This gives $$ 3OG^2 - 3O_9G^2 = 3\left(\frac 23\right)^2O_9H^2 -3\left(\frac 13\right)^2O_9H^2 = 3\left(\frac 43-\frac 13\right)O_9H^2 = O_9H^2\ . $$ Putting all together, we get $\sum O_9A^2+O_9H^2=3R^2$.

$\square$

Answer 2

Write $N$ for the nine-point center of the triangle $ABC$, and $O$ for the circumcenter. Let $M_a$, $M_b$, and $M_c$ be the midpoints of $BC$, $CA$, and $AB$, respectively. Use Stewert's Theorem or Law of Cosines to establish that $$NB^2\cdot M_aC-NM_a^2\cdot BC+NC^2\cdot BM_a-M_aC\cdot BC\cdot BM_a=0\,.$$ Since $M_aC=BM_a=\dfrac12BC$, we have $$NM_a^2=\frac{NB^2+NC^2}{2}-\frac14BC^2\,.$$ However, $N$ is the circumcenter of the triangle $M_aM_bM_c$, which is similar to the triangle $ABC$ via a homothethy centered at the centroid $G$ of the triangle $ABC$ with the scaling factor $-\dfrac12$. Therefore, $NM_a$ is the circumradius of the triangle $M_aM_bM_c$, which is half the circumradius of the triangle $ABC$, namely, $NM_a=\dfrac12 R$. This gives $$\frac{R^2}{4}=\frac{NB^2+NC^2}{2}-\frac14BC^2\,.$$ We also have two similar equations: $$\frac{R^2}{4}=\frac{NC^2+NA^2}{2}-\frac14CA^2$$ and $$\frac{R^2}{4}=\frac{NA^2+NB^2}{2}-\frac14AB^2\,.$$ Combining all three of them yields $$NA^2+NB^2+NC^2-\frac{1}{4}(BC^2+CA^2+AB^2)=\frac{3R^2}{4}\,.$$ From this past question, $$BC^2+CA^2+AB^2=9R^2-OH^2\,.$$ Therefore, $$NA^2+NB^2+NC^2-\frac14(9R^2-OH^2)=\frac{3R^2}{4}\,,$$ which is equivalent to $$NA^2+NB^2+NC^2-\frac{OH^2}{4}=3R^2\,.$$ By Euler's Theorem, $N$ bisects $OH$; therefore, $\dfrac{OH}{2}=NH$, making $$NA^2+NB^2+NC^2-NH^2=3R^2\,.$$

Answer 3

Complex Proof: Place the points $A, B, C$ across the unit circle on the argand plane with the coordinates $a, b, c$. Then $$|a|=|b|=|c|=R^2=1$$ $$H:a+b+c$$ $$O_9:\frac{a+b+c}{2}$$

Using dot product of complex numbers, we obtain $$O_9A^2+O_9B^2+O_9C^2+O_9H^2$$ $$=\frac{(b+c-a)\cdot(b+c-a)}{4}+\frac{(c+a-b)\cdot(c+a-b)}{4}+\frac{(a+b-c)\cdot(a+b-c)}{4}+\frac{(a+b+c)\cdot(a+b+c)}{4}$$ $$=\frac{4 (a\cdot a+b\cdot b+c\cdot c)}{4}$$ $$=|a|+|b|+|c|$$ $$=\boxed{3R^2}.$$

Synthetic Proof: By Leibniz Theorem, we have: $$PA^2+PB^2+PC^2-3PG^2=GA^2+GB^2+GC^2.$$ If $P \equiv O$ (the circumcenter of $\Delta ABC$), then: $$OA^2+OB^2+OC^2- 3OG^2=GA^2+GB^2+GC^2.$$ $$\text{i.e.}\;GA^2+GB^2+GC^2 = 3R^2-3OG^2.$$ If $P \equiv O_9,$ then: $$O_9A^2+O_9B^2+O_9C^2-3O_9G^2=GA^2+GB^2+GC^2=3R^2-3OG^2.\;\;\;(1)$$ But the points $H,O_9,G$ & $O$ are collinear, in this order on the Euler line. $O_9$ is the midpoint of $OH,$ and $$\frac{HG}{GO}=2$$ $$\implies O_9G=\frac{1}{3}OO_9=\frac{1}{3}O_9H$$ $$\implies OG^2-O_9G^2=\frac{4}{9}O_9H^2-\frac{1}{9}O_9H^2=\frac{1}{3}O_9H^2\;\;\; (2)$$ From $(1)$ and $(2)$, the desired result follows.