Proving that $\lim_{x \to 0} \frac{\sin(x)}{x} = 1$

Question

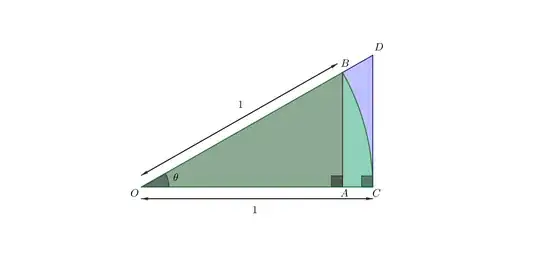
So, I'm trying to prove the following assertion:

$\lim_{x \to 0} \frac{\sin(x)}{x} = 1$

---

Proof Attempt:

Let $\epsilon > 0$. Then, we have to show that:

$$\exists \delta > 0 : 0 < |x| < \delta \implies |\frac{\sin(x)}{x} - 1| < \epsilon$$

Let us consider the following:

$$\cos(x) < \frac{\sin(x)}{x} < 1$$

if $0 < |x| < \frac{\pi}{2}$. So, we have:

$$0 < 1 - \frac{\sin(x)}{x} < 1 - \cos(x) = 2\sin^2(\frac{x}{2}) \leq 2 |\sin(\frac{x}{2})| \leq |x| < \delta$$

That's, of course, assuming that $0 < |x| < \frac{\pi}{2}$.

If $\epsilon \geq \frac{\pi}{2}$, then let $\delta = \frac{\pi}{2}$. This would ensure that $1-\frac{\sin(x)}{x}$ is still greater than 0.

If $\epsilon < \frac{\pi}{2}$, then let $\delta = \epsilon$. This would still mean that $0 < |x| < \delta < \frac{\pi}{2}$ so the inequality above would still be satisfied.

This proves the given assertion.

Could someone check my proof above and see if it works or not?

Answer 1

Let's prove an inequality using some geometry :

Let $ \theta \in\mathbb{R} \cdot $ Observe the following figure :

Denoting $ \mathscr{A} $ the red region, (The triangle $ OBC $), $ \mathscr{B} $ the green one, (A part from the unit disc that has a circumference of $ \theta $), $ \mathscr{C} $ the ble one, (The triangle $ OCD $). $ \mathscr{S}_{\mathscr{A}} $, $ \mathscr{S}_{\mathscr{B}} $ and $ \mathscr{S}_{\mathscr{C}} $ are their respective areas.

We have : \begin{aligned} \mathscr{S}_{\mathscr{A}}\leq\mathscr{S}_{\mathscr{B}}\leq\mathscr{S}_{\mathscr{C}}\ \ \ \ \ \\ \iff \frac{\sin{\theta}\cos{\theta}}{2}\leq\frac{\theta}{2}\leq\frac{\tan{\theta}}{2}\ \ \ \\ \iff \ \ \ \ \ \ \ \cos{\theta}\leq\frac{\sin{\theta}}{\theta}\leq\frac{1}{\cos{\theta}}\end{aligned}

Meaning, we have $ \lim\limits_{\theta\to 0}{\frac{\sin{\theta}}{\theta}}=1 \cdot $

Answer 2

First change the name of the variable to $\theta,$ so we have to prove $$\lim_{\theta\to 0}\frac{\sin \theta}{\theta}=1.$$ Take a point $(x,y)$ on the unit circle in the first quadrant. The proof is almost the the same for a point in the 4-th quadrant. Then $\theta$ is the arc length from $(x,y)$ to (1,0) and $\sin \theta=y.$ We need bounds on the arc length. For a non-negative integer $n$ divide the interval $[x,1]$ into $2^n$ equal sub-inervals. Note that we deliberately include the case $n=0$ when the interval is left in one piece. For each division point $x_i$ on the X-axis let $P_i=(x_i,y_i), 0 \le i \le 2^n$ be the corresponding point on the unit circle so that $P_0=(x,y)$ and $P_{2^n}=(1,0).$ For $n \ge 0$ let $$S_n=\sum_{j=1}^{2^n}\text {straight-line lengths from $P_{j-1}$ to $P_j$}.$$ The triangle inequality shows that $S_0,S_1, ...$ is an increasing sequence and that $$S_n \le 1-x+y$$. Thus $\lim_{n \to \infty}S_n$ exists. We define the arc length=$\theta=\lim_{n \to \infty}S_n$Then $$\sqrt{(1-x)^2+y^2}=S_0 \le \theta \le 1-x+y$$. $$\sqrt{(1-\sqrt(1-y^2))^2+y^2}\le \theta \le 1-\sqrt(1-y^2)+y$$ The conditions $\theta \to 0$ and $y \to 0$ are equivalent. All that is needed now is to take the reciprocals in our upper and lower bounds for $\theta$, multiply through by $\sin \theta$, which is the same as $y$ to obtain upper and lower bounds on $\frac {\sin \theta}{\theta}$ in terms of $y.$ With the squeeze law for limits and a little algebra, you can finish the proof.