There are at least two questions on this site related to the (somewhat famous) false proof that all triangles are isosceles as presented for example in M. J. Greenberg's 'Euclidean and Non-Euclidean Geometry'. The fallacy itself can be read on this site here:
What is the flaw in this proof that all triangles are isosceles?
Although the answers for both of these questions give the correct reason that there is an incorrect assumption of 'betweenness' leading to the fallacy, I have not seen an attempt to prove the betweenness part of the fallacy itself, which is the crux of the matter (excuse me if I overlooked something in the other two answers).
I struggled to come up with a proof for the betweenness part of the fallacy. I had added an early version of this effort as an answer to one of the other two questions earlier, but did not get any feedback. I think this betweenness part deserves a separate question: Can anyone critique the basic steps of my proof as given here and/or give a proof for the betweenness part of the fallacy?
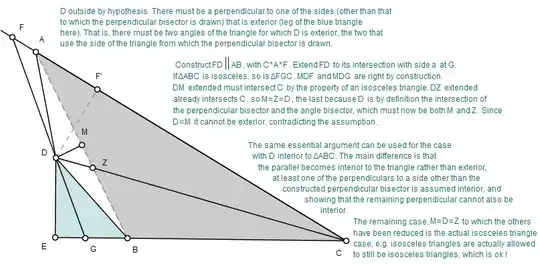
The diagram covers 'case 4' of the false proof, that the intersection of the perpendicular bisector and the angle bisector are at a point D exterior to the triangle. The other false case of D interior is similar, which I describe in the diagram text. I have left the last case, that D is on the triangle (even though the perpendicular bisector and angle bisector do not coincide) aside for now, but if the argument I give here is correct, I think it too will be an extension of the same idea.