Prove that $$ \left(\sqrt x, \sqrt{x + \sqrt x}, \sqrt{x + \sqrt {x + \sqrt x}}, \ldots\right)$$ in $[0,\infty)$ is convergent and I should find the limit function as well.
For give a idea, I was plotting the sequence and it's look like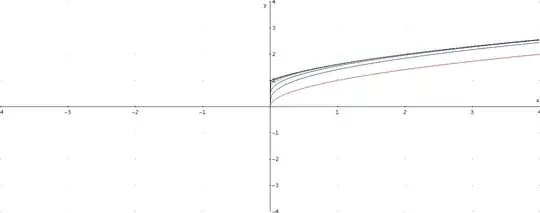
Prove that $$ \left(\sqrt x, \sqrt{x + \sqrt x}, \sqrt{x + \sqrt {x + \sqrt x}}, \ldots\right)$$ in $[0,\infty)$ is convergent and I should find the limit function as well.
For give a idea, I was plotting the sequence and it's look like
Hint: The limit function $f$, where it exists, should satisfy $(f(x))^2=x+f(x)$.
For existence, perhaps use the fact that an increasing sequence that is bounded above converges.
Note that $f(x)$ is limited by $\sqrt{x}+1$ as can be shown easily by $induction$.
For the limit $y=f(x)$ we have the following :
$\sqrt{x+y}=y$
$x+y=y^2$
$0=y^2-y-x$
$\Delta= 1+4x $
$ So $ , $y=f(x)=\frac{1+\sqrt{1+4x}}{2}$ for $x>0$ and $f(0)=0 $ .