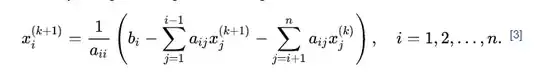Implementing Jacobi and Gauss-Seidel Method

Question

I am implementing the Jacobi Method and the Gauss-Seidel Method in the C programming language right now.

I successfully implemented the Jacobi Method and am getting the correct results for each iteration, but currently I struggle with implementing the Gauss-Seidel Method.

If I implemented both algorithms according to their pseudocode on wikipedia:

(Gauss-Seidel Method Algorithm)

(Jacobi Method Algorithm)

...then I would end up with the same implementation in the C programming language.

Both method obviously differ from one another, so instead of looking at the algorithms on wikipedia I instead decided to implement the methods by looking at their formulas.

(Gauss-Seidel Formula)

But my program code below doesnt work as intended yet. I get the wrong results for x^(k+1)

Here is my current source code:

maxIterations = 50;
A = Matrix;
b = Vector;
x = xNew = Vector;

for(int iteration = 0; iteration < maxIterations; iteration++) {

            for(int i = 0; i < n; i++) {
                    double sum1 = 0.0, sum2= 0.0;

                    for(int j = 0; j < (i - 1); j++) {
                            sum1 += A->data[i][j] * xNew->data[j];
                    }

                    for(int j = (i + 1); j < n; j++) {
                            sum2 += A->data[i][j] * x->data[j];
                    }

                    xNew->data[i] = (1/A->data[i][i]) * (b->data[i] - sum1 - sum2);
            }

            for(int i = 0; i < n; i++) {
                    x->data[i] = xNew->data[i];
            }

    }

Can somebody please tell me how my code differs from the Gauss-Seidel formula?

score 1 · Answer 1 · answered Mar 22 '20 at 15:55

Since you have $i$ and $j$ starting from $0$ you used $<$ instead of $\le$ in the upper limit. That's fine. But you need to adjust the lower limit. When you start from $0$ it's fine. But the last term starts from $j=i+1$. You forgot to account for this.

Implementing Jacobi and Gauss-Seidel Method

1 Answers1