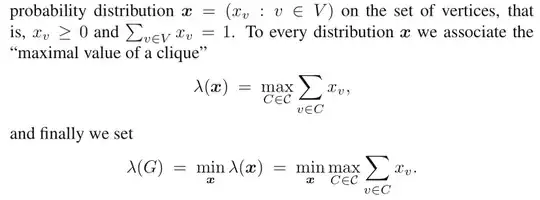The first principles of duality in LP state simply that if you have a primal problem of the following form
Then i can write the dual LP automatically as:
Let $\mathcal{C}$ be the set of cliques in G. Consider an arbitrary
Now how do we write the dual of this bi-level LP? The answer is as follows:
Is there some graph theory trick that I am missing? The dual transformation seems hand-wavy. I am not able to derive it from the first principles as shown above.
EDIT:
I am trying to expound on Misha's answer. There are gaps in my understanding which can hopefully be filled.
In below $z$ is a scalar. $\mathbf{x}\in R^{|V|}$ is a vector. We wish to minimize
$\underset{\mathbf x, z}{\text{min}}\ z$
Now i want to map this to the vanilla model. So $p$ is a vector of $1$ followed by $|V|$ number of zeros, and $x$ is really $z$ concatenated with our probability distribution $\mathbf{x}$. If any symbol is not clear go back to start of the question where i have clearly defined these terms.
Now let me write the constraints one by one as inequalities because i still do not have the hang of equalities in LP, and then I will try to write out the $A$ matrix.
$z - \sum_{v \in C} x_v\ge 0 \text{ for all }C \in \mathcal C$
$\sum_{v \in V} x_v \ge 1$
$-\sum_{v \in V} x_v \ge -1$
And the constraints on the variables are simply:
$z \ge \mathbf 0, \mathbf x \ge \mathbf 0$
Now i want to write down my matrix $A$ and vector $b$ so that from there the dual transformation is straightforward and there is no scope for confusion.
It is clear that $A\in R^{(|\mathcal{C}|+2)\times (|V|+1)|}$ and $b\in R^{(|\mathcal{C}|+2)}$.
Let us first fill $A$ row by row. The first row will be $1$ followed by $|V|$ numbers, some of which will be $-1$ and some will be zero depending on which clique we are considering at that row. Now let us focus on the penultimate row. The first term will be zero followed by $|V|$ numbers of $1$. The last row similarly will have first term as zero followed by $|V|$ numbers of $-1$.
Now we try to write out $b$ which is simply $|V|$ numbers of zeros followed by $1$ and $-1$. Now to perform dual transformation I do need the dual variable to $x$. Please note that $x$ and $\mathbf{x}$ are different things here due to a suboptimal choice of notations in the beginning.
What is the dual variable of $x$? Say it is $w\in R^{|\mathcal{C}|+2}$. So dual problem requires us to maximize as follows:
$\underset{w}{\text{max}}\ b'w$
And $b'w$ is just the difference of the last two terms of $w$ due to structure of $b$. Now there will be $|V|+1$ inequality constraints. But now i am getting confused how to reconcile this with the final answer. Can someone fill the rest? i am trying to make use of this post.