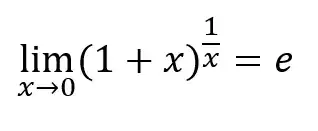1

I'm solving some limits and in one of my examples I need to use the fact that:

enter image description here

I am, however, unable to prove that this is actually true. I believe I can't just substitue t=(1/x) because than we can not say where such t is going. I tried to find the proof online, but they all rely on L'Hôpital's rule, which I am trying to avoid. How can I prove this equality without it?

Jesus
  • 1,798
  • You dont. It's the definition of $e$. You can prove it converges to something (by noting it is bounded above yet increasing. Then you declare that what it converges to is $e$. – fleablood Mar 14 '20 at 17:11
  • What I'm trying to show is that it follows from lim(x->∞)(1+(1/x))^x. This is my definition of e. – Jesus Mar 14 '20 at 17:13
  • Just replace $\frac 1x$ with $y$. As $\lim_{y\to \infty}(1+\frac 1y)^{y} = \lim_{x\to \infty}(1+ x)^{\frac 1x}=e$ – fleablood Mar 14 '20 at 17:16
  • But where is y going then; is it going towards ∞ or -∞? If we define y like that (y=1/x as x->0), it does not converge? – Jesus Mar 14 '20 at 17:18
  • Do both. $\lim_{x\to 0^-} (1+x)^{\frac 1x} = \lim_{x\to 0^+}\frac 1{(1-x)^{\frac 1x}}=\lim_{y\to -infty}(1 + \frac 1y)^{y}$ And $\lim_{x\to 0^+}(1+x)^{\frac 1x}\lim_{y\to +infty}(1 + \frac 1y)^{y}$. Show they that $\lim_{y\to -infty}(1 + \frac 1y)^{y}=e$. – fleablood Mar 14 '20 at 17:37
  • Just to make sure, if I do both, is the proof then correct and complete? – Jesus Mar 14 '20 at 17:40
  • All of the standard / well known limits which deal with symbols like $e, e^x, a^x, \log$ can't be proved without a proper theory which encompasses all these symbols. Unfortunately by an act of intellectual dishonesty the theory is never provided in many introductory calculus texts. Common justification is that the theory is difficult for beginners. Point taken! But then honestly one should declare "the theory of these symbols is complicated for beginners and you can accept these limit formulas without proof. Don't try to prove them unless you have learnt the corresponding theory". – Paramanand Singh Mar 14 '20 at 19:00

3 Answers3

2

Write it as $(1+\frac{1}{n})^n$ and get the binomial expansion $\sum_{k=0}^n\frac{n(n-1)...(n-k+1)}{n^k}\frac{1}{k!}$. As $n\to \infty$, expansion converges to infinite series for $e=\sum_{k=0}^\infty\frac{1}{k!}$

Note: this is way I first learnt it in high school.

herb steinberg
  • 12,765
1

We will first prove a supporting result using sandwich theorem

$$ \begin{align} \frac{x}{x+1} &< \ln(1+x) < x &\text{for $x > -1$} \end{align} $$ See this reference.

$$ \lim_{x \to 0} \frac{1}{x+1} < \lim_{x \to 0} \frac {\ln(1+x)}{x} < \lim_{x \to 0} 1 $$

$$ \Rightarrow \lim_{x \to 0} \frac {\ln(1+x)}{x}=1 $$

And now we can solve the limit in the question. $$ \lim_{x \to 0}(1+x)^{\frac{1}{x}} = e^{\lim_{x \to 0}\frac {\ln(1+x)}{x}}=e $$

ratsalad
  • 133
  • 5
Mathsmerizing
  • 2,003
1

Let $g(y) = \frac 1y$. $\lim_{y\to \infty} g(y) = 0$. Thus if $\lim_{k\to\infty} f(k) = \lim_{g(k)\to 0} f(k)$.

$\lim_{x\to 0}(1 + x)^{\frac 1x}$. Replace $x$ with $g(y)$

$\lim_{g(y)\to 0}(1+g(y))^{\frac 1{g(y)}}=$

$\lim_{g(y)\to 0}(1+\frac 1y)^y=$

$\lim_{y\to \infty}(1+\frac 1y)^y =e$

fleablood
  • 124,253