1

I have the following integral

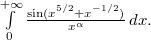
and I need to find maximum integer $\alpha$ for which the integral converges.

I think that I need to reduce this integral to the Dirichlet integral

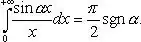
enter image description here

with some special substitution. I've tried different variants of them, but this leads me to the cumbersome calculations.

Can somebody help me to reduce the integral to the Dirichlet form?

Or should I solve this problem in completely different way?

Ann Orlova
  • 357
  • 1
    You should only have to worry about $0$, I think. The behavior of the $x^{-1/2}$ term dominates there, so my guess would be $\alpha = 0$ works, but not $\alpha = 1$. I'm not sure how to make this argument rigorous yet. On second thought, the integral goes bad at $\infty$ for $\alpha = 0$. – Paul Gustafson Apr 11 '13 at 07:46

1 Answers1

1

Considering the integral from $0$ to $1$, substituting $x=u^{-2}$ gave me $2\int\limits_{1}^\infty \sin\left(u+u^{-5}\right) u^{2\alpha-3} du$. For it to converge we need $2\alpha-3<0$, so I think your answer is $\leq 1$, and as user66345 said $\geq 0$.

ronash
  • 201
  • Also this answer was helpful http://math.stackexchange.com/questions/358434/to-determine-whether-the-integral-int-0-infty-frac-sinaxbxp-m – Ann Orlova Apr 12 '13 at 07:17