11

At the moment I'm doing a project about the Smale horseshoe map. This is a function which maps a square $D= \{(x,y)\in \mathbb{R}^2: 0\le x\le 1,\text{ } 0\le y \le 1 \} $ to a 'horseshoe'. It contracts in the $x$-direction, expands the $y$-direction and folds around, like in the picture:

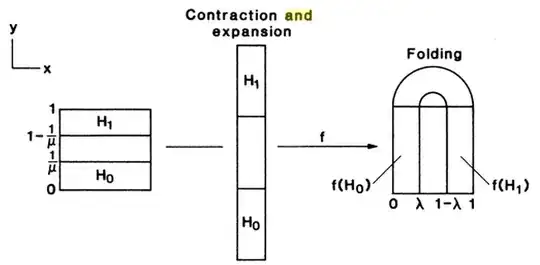
enter image description here

The goal of the text is to study the invariant set under $f$: we are interested in the points which will stay forever in $D$ if you apply $f$ or $f^{-1}$ arbitrary often. That is, we want to look at the set $...\cap f^{-1}\cap D\cap f(D)\cap f^2(D)\cap ...$

Therefore, it's only necessary to define the function for $H_0$ and $H_1$, because the other elements are being mapped outside $D$, so we can just ignore those. $H_0, H_1$ can be described as:

\begin{equation} H_0= \{(x,y)\in \mathbb{R}^2: 0\le x\le 1, \text{ } 0\le y \le 1/{\mu} \} \end{equation}

\begin{equation} H_1= \{(x,y)\in \mathbb{R}^2: 0\le x\le 1, \text{ } 1-1/{\mu} \le y \le 1 \} \end{equation}

Then, the definition of those subsets is as follows:

\begin{equation} H_0: \begin{pmatrix} x \\y \end{pmatrix} \mapsto \begin{pmatrix} \lambda & 0 \\ 0 & \mu \end{pmatrix} \begin{pmatrix} x \\y \end{pmatrix} \end{equation}

\begin{equation} H_1: \begin{pmatrix} x \\y \end{pmatrix} \mapsto \begin{pmatrix} -\lambda & 0 \\ 0 & -\mu \end{pmatrix} \begin{pmatrix} x \\y \end{pmatrix} + \begin{pmatrix} 1 \\\mu \end{pmatrix} \end{equation}

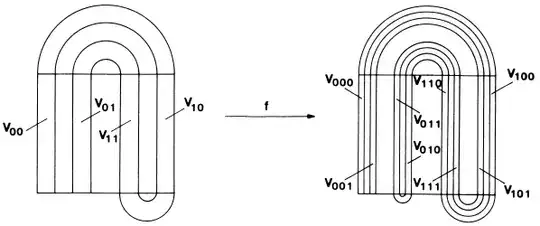
If we keep applying $f$ on the domain, the set $D\cap f(D) \cap f^2(D) \cap ...$ will develop as follows: enter image description here

While if we keep applying $f^{-1}$ we get the following result:

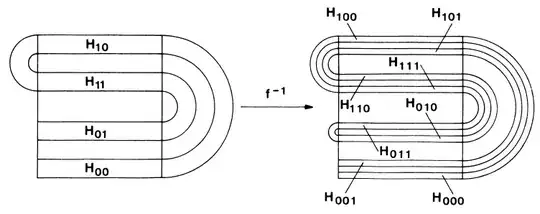
enter image description here

As you can see, if we take the intersection of both, and letting the number of iterations go to infinity, we get intersections of horizontal and vertical rectangles, which are just points.

So, now my question is: What's the point of this? What are the theoretically interesting aspects of this map? What applications are there for this map?

jyalim
  • 105
Applied mathematician
  • 3,186

3 Answers3

12

The horseshoe map is one example of a discrete-time dynamical system with interesting properties. Consider what happens with two points $x_1$ an $x_2$ which are arbitrarily close together and track their images under iterated application of the horseshoe map. Are their orbits (i.e. the sets $\{f^n(x_i)\}_{n=1,2,\dots}$ related? Do they stay close together? In fact they don't. The dynamics of this map is chaotic, consider the Wikipedia page for further clarification.

By the way: Have you ever tried to mix two colors of colored putty? To simply "knead" randomly will not do very good. However, something "horseshoeisch", i.e. folding and squashing, will give a great mix quickly. Similarly, this is the way how bakers work on their dough and this coincidence is not by accident.

Dirk
  • 11,680
  • 3
    +1 for teaching me something new today (about baking, that is). It never occurred to me to apply dynamical systems to dough kneading. – Willie Wong Apr 10 '13 at 12:59
5

The point of horseshoe is to demonstrate the phenomenon of "chaos". It is a simple model which reproduces the most complex (symbolic) dynamics found in nature. There is a fundamental theorem in dynamical systems which states that horsheoes are generically (i.e. ALWAYS) present in a system with transversal intersection of heteroclinic or homoclinic manifolds of hyperbolic points. I would suggest looking at Wiggin's Nonlinear dynamical systems and chaos book for an excellent treatment. He develops the horseshoe->then gives the conditions under which a horseshoe is present in a system (called Conley-Moser conditions)->then proves that given a hyperbolic point with transversal intersections of invariant manifolds, the Conley-Moser conditions are satisfied.

nonlinearism
  • 2,065
1

Several years on, there is an excellent Scholarpedia article (http://www.scholarpedia.org/article/Smale_horseshoe) on the Horseshoe map, which really explains well what it is good for:

The utility of Smale's analysis is this: every dynamical system having a transverse homoclinic point, such as r , is such that some power f^T has also a horseshoe containing r , and has thus the shift chaos. Nowadays, this fact is not hard to see, even in higher dimensions. The mere existence of a transverse intersection between the stable and unstable manifolds of a periodic orbit implies a horseshoe. In the case of flows, the corresponding assertion holds for the Poincare map. To recapitulate, transverse homoclinicity ⇒ horseshoe ⇒ chaos.

And another important defining feature of the map its hyperbolicity. Read the link to know more.

ap21
  • 253