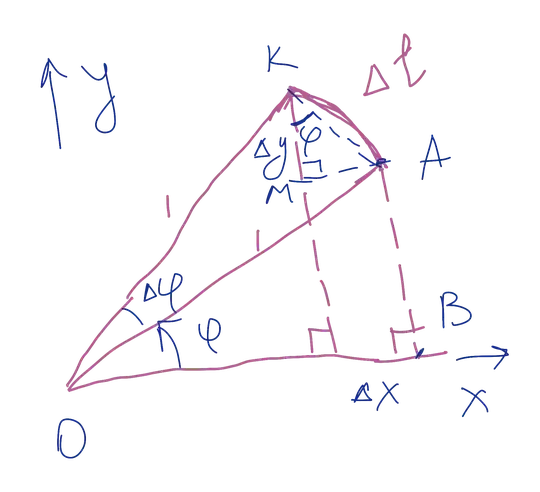
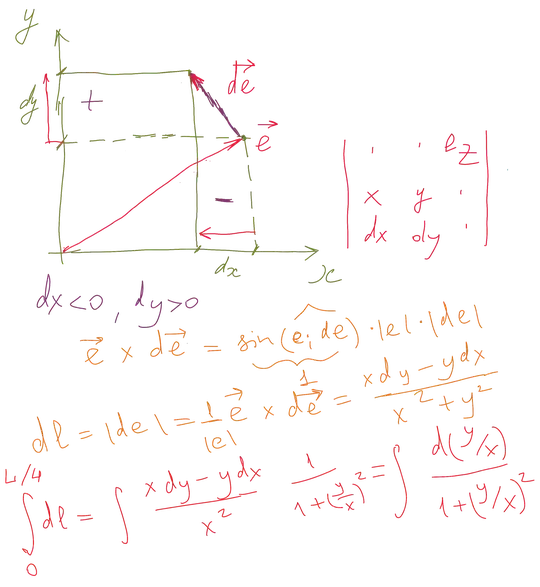3

When I was on the road today I came across one interesting puzzle.

What if you meet an extraterrestrial species, and you show to them some of mathematical works. They look at $\pi$ and they clearly don't understand what it means. So they ask you, and you write $x^2 + y^2 = 1$ and say, "Look, $\pi$ comes from it."

How to show the exact details? What way will be shorter and why?

I came up with 3 basic ways but none of them is easy, each of them involves some geometry. But universally there have to be built some trigonometry around, otherwise at integration/differentiation there would be misunderstanding of arcsin/arctan functions. Also $\lim\frac{\sin x}{x}$ have to be built somehow, and geometry is best suited for it.

Is there any way to do it without geometry at all? What is the shortest path from $x^2+y^2=1$ to $\pi$?

Community
  • 1
sanaris
  • 253
  • In regards to your (previous) title: $\pi$ is transcendental, not algebraic – J. W. Tanner Mar 03 '20 at 14:52
  • Yea, I know I used bad wording – sanaris Mar 03 '20 at 14:55
  • First of all, you should define $\pi$ in some way. If you define it as the "length of the circunference", you should probably need something like a limit or the integral of a derivative to understand what the "length of a curve" is. Same questioning may happen if you define it using areas. Tell me what definition of $\pi$ you are using and what is within the scope of "admisible" steps when reading $\pi$ off that circunference equation. – Luis Ferroni Mar 03 '20 at 14:57
  • To give you an example: if you like the arc length stuff, you can write $y=\sqrt{1-x^2}$ from your equation. That defines a function on $[-1,1]$ whose arc length is exactly $\pi$. Hence if you call $f(x)=\sqrt{1-x^2}$ you just have: $$\pi = \int_{-1}^1 \sqrt{1+f'(x)^2} dx$$ – Luis Ferroni Mar 03 '20 at 15:06
  • For other interesting and unexpected applications of $\pi$ see this question: https://math.stackexchange.com/questions/689315/interesting-and-unexpected-applications-of-pi – Anton Vrdoljak Mar 03 '20 at 15:16
  • To do it without geometry, does it make sense to essentially just rely on the formal definitions of limits, derivatives, and integrals and then show how $pi$ comes out from these equations? Essentially, figure out how you'd explain it with geometry but just write everything out using equations and don't use the geometric intuition at all. – roundsquare Mar 03 '20 at 15:19
  • @J.W.Tanner : To say the least, it is anything but clear that the earlier title of this thread could reasonably be construed to mean that $\pi$ is algebraic. – Michael Hardy Mar 03 '20 at 15:50

2 Answers2

4

We can compute the length of the circumference of a unit half-circle with

$$x^2+y^2=1\implies 2x+2yy'=0$$ so that $$\text{Pi}=\int_{-1}^1\sqrt{1+y'^2} \, dx = \int_{-1}^1 \frac{dx}{\sqrt{1-x^2}}.$$

Then by Taylor,

$$\frac1{\sqrt{1-x^2}}=\sum_{k=0}^\infty\frac{(\frac12-k)!}{k!} x^{2k}$$

and

$$\text{Pi}=2\sum_{k=0}^\infty\frac{(\frac12-k)!}{(2k+1)k!}.$$

Michael Hardy
  • 1
1

I have come to really marvellous high-school tier single-step solution which routes to the same Leibnitz series, but involves only one step with both geometry and vector multiplication.

enter image description here

Below is typeset

$$ \mathbf{e} \times \mathbf{de} = \sin(\hat{e;de})\cdot|e|\cdot|de| $$ $$ dl = |de| = \frac{1}{|e|} \mathbf{e}\times\mathbf{de}=\frac{x\,dy-y\,dx}{x^2+y^2} $$ $$ \int_0^{L/4}dl=\int\frac{1}{1+\left(\frac{y}{x}\right)^2}\frac{x\,dy-y\,dx}{x^2}=\int_0^1 \frac{d(y/x)}{1+(y/x)^2} $$

Below is classic Leibnitz solution (3 steps). Leibnitz tangent solution

  1. Consider $\triangle OAB \propto \triangle AKM $ so for sides when we obtain infinitesimally small $\triangle AKM$, we got $$\frac{-dx}{y}=\frac{dy}{x}=\frac{dl}{1}=\frac{d\phi}{\kappa},$$ here we acknowledge that angles are proportional to arc with coefficient $\kappa$ because we able to stack many equal triangles together. I tried to exclude this geometry step somehow but it seems extending the whole thing.

  2. Now we define our ratio for alien (tangent func) as $t=\frac{y}{x}$. From (1) and next with integration it follows $$\frac{dx}{d\phi}=\frac{-y}{\kappa},\frac{dy}{d\phi}=\frac{x}{\kappa}.$$ $$\frac{dt}{d\phi}=\frac{y'x-yx'}{x^2}=\frac{x^2+y^2}{\kappa x^2}$$ $$\frac{d\phi}{dt}=\kappa x^2=\frac{\kappa}{1+t^2}$$

  3. Now we denote straight angle $\phi_0$, arc $L$, we know that $t=1$ at one forth of it from symmetry considerations. Here we get Leibnitz: $$\int_0^{L/4} dl = \int_0^{\phi_0/4} \frac{d\phi}{\kappa} = \int_0^1 \frac{dt}{1+t^2}.$$

$$\pi=L=\frac{\phi_0}{\kappa}=4 \sum_{k=0}^{\infty} \frac{(-1)^k}{2k+1} $$

sanaris
  • 253