Is Pythagoras' Theorem a theorem?

Question

From a foundations/logic perspective, for one to prove Pythagoras' theorem, one would require the definition $$d(\boldsymbol x, \boldsymbol y) = \sqrt{(x_1-y_1)^2 + \cdots + (x_n - y_n)^2}$$ of distance in the first place, which embeds Pythagoras' theorem within it, so to call it a theorem seems a bit circular (although you could nitpick and prove the case for a right-angled triangle which is rotated and whose right-angle is not aligned with the coordinate axes). But basically Pythagoras' theorem is already encoded in the definition.

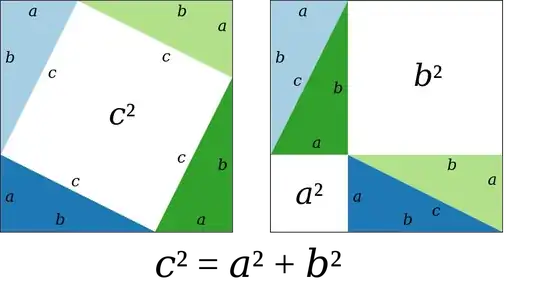
So my question is, when we see "proofs" of Pythagoras such as the famous one below,

what are we proving exactly? Or, more precisely, what axioms are we building off so that this is considered a proof? Is there some logical framework in which this can be considered a real proof?

My guess is that this is simply something to aid our intuition and is based off our perception of the real world, and is in fact circular. Or perhaps it's based off something vague like Euclid's axioms.

Edit: For clarity,

I am mainly interested in whether the typical proofs we see are actually doing anything, in the modern sense. Allegedly there are hundreds of proofs of Pythagoras' theorem, some quite clever, but are they meaningful in any modern way?

You can't just define some function to be a distance. You have to show that it fullfills some stuff distances should fullfill. — Luke, Mar 02 '20 at 13:36
Pythagoras's theorem does not have associated coordinates. Euclid stated it in Proposition 47 of Book 1 of his Elements as something like "In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle" and proved it from his earlier axioms and postulates — Henry, Mar 02 '20 at 13:36
https://mathcs.clarku.edu/~djoyce/java/elements/bookI/propI47.html — Xander Henderson, Mar 02 '20 at 13:36
@Luke Well of course $d$ is a metric so that $(\mathbb R^n, d)$ is a metric space, but that does not shed light on Pythagoras' theorem. — Luke Collins, Mar 02 '20 at 13:37
@Henry Euclid's elements, although very significant historically, is not based on logically sound axioms in the modern sense. — Luke Collins, Mar 02 '20 at 13:38
I believe the Theorem preceded the definition of distance that you give, since the latter uses Cartesian coordinates. — Sort of Damocles, Mar 02 '20 at 13:38
One does not need a metric to prove or state the Pythagorean theorem. In modern mathematics, the statement is more akin to one in measure theory (it is about the areas of squares, after all), though Euclid's definitions build the theory slightly differently. — Xander Henderson, Mar 02 '20 at 13:38
@LukeCollins Off the top of my head, I am not entirely certain. As you say, Euclid's treatment is not entirely rigorous by modern standards. However, note that Euclid's proof never describes any kind of distance; instead, he uses area preserving transformations (e.g. the Principle of Cavalieri) to transform the two squares on the legs into the square on the hypotenuse. — Xander Henderson, Mar 02 '20 at 13:45
The key ideas used in Euclid's proof are notions of orthogonality; if you have a space where orthogonality makes sense, I suspect that one can seek to verify the Pythagorean theorem in a manner similar to Euclid's. On the other hand, if you live in a space with a Pythagorean theorem, then the space possesses a metric which is induced by the identity. — Xander Henderson, Mar 02 '20 at 13:50
@XanderHenderson I am mainly interested in whether the typical proofs we see are actually doing anything, in the modern sense. Allegedly there are hundreds of proofs of Pythagoras' theorem, some quite clever, but are they meaningful in any modern way? — Luke Collins, Mar 02 '20 at 13:50
@XanderHenderson Indeed, how in an IPS, you get $|x+y|^2 = |x|^2 + |y|^2$ when $\Re\langle x,y\rangle = 0$. — Luke Collins, Mar 02 '20 at 13:53
@LukeCollins: "Euclid's elements, although very significant historically, is not based on logically sound axioms in the modern sense." ... True, but modern axiomatic systems like Hilbert's fill in the gaps left by Euclid. (The gap-filling amounts to better bookkeeping about continuity and betweenness and such. The Euclidean flavor remains.) So, it isn't necessary to abandon "synthetic" geometry for coordinates when seeking a sound logical foundation for the subject in general or Pythagoras' result in particular. — Blue, Mar 02 '20 at 14:22
@LukeCollins But one doesn't need to construct the structure of an inner product space in order to prove Pythagoras's theorem in $\mathbb{E}^2$ (two-dimensional Euclidean space). — Xander Henderson, Mar 02 '20 at 14:22
@Blue Interesting, I had heard but forgot about Hilbert's axioms. — Luke Collins, Mar 02 '20 at 14:34
@XanderHenderson How would you get the notion of orthogonality? — Luke Collins, Mar 02 '20 at 14:35
Hartshorne's Euclidean geometry book is good at answering this kind of question. As I recall, the conclusion I came to from reading it is that not all proofs of the Pythagorean theorem are doing the same thing! This is because there are two different ways to encode multiplication in Euclidean geometry: as a statement about areas or as a proportionality relation. Some proofs of the Pythagorean theorem are much more naturally interpreted one way, and some the other. — Micah, Mar 02 '20 at 16:07
(Of course these two interpretations can eventually be shown to be equivalent, but the proof of equivalence is more complicated than the standard Pythagorean proofs...) — Micah, Mar 02 '20 at 16:08

Ethan Bolker · Accepted Answer · 2023-02-05T15:06:00.037

Any mathematical system, and geometry in particular, is logically just a sequence of deductions from a set of axioms.

The Pythagorean Theorem follows from Euclid's axioms for geometry. That was true in Euclid's time even though the axioms he used are not "logically sound" by modern standards. It's still true today when you use contemporary axioms.

In fact, the Pythagorean Theorem is just one of many theorems in geometry that are equivalent to the famous fifth postulate on parallel lines - see https://www.cut-the-knot.org/triangle/pythpar/PTimpliesPP.shtml . If you study any of the non-Euclidean geometries in which the parallel postulate fails, the Pythagorean Theorem will fail there too.

To connect the geometric content of the Pythagorean Theorem to the notion of distance between points given in the usual coordinate system in the plane you have to define a coordinate system. Doing that requires the parallel postulate. If your geometry starts from the usual coordinate system then you have implicitly assumed the parallel postulate in such a way that the Pythagorean Theorem does seem obvious, so not in need of the many proofs in the literature.

Noah Schweber · Answer 2 · 2020-03-02T19:52:12.887

Building off of Ethan Bolker's answer, it may be helpful to see how Pythagoras' theorem can be stated in the language of "pure geometry:"

First, we pin down how to identify right angles. Suppose $A,B,C$ are non-collinear. Then we say $\angle ABC$ is a right angle iff the reflection of $C$ across $AB$ is on the line $\overline{BC}$. (We could also talk about adding angles, but we don't have to here.)
With right angles in hand, we can talk about squares: a square is simply a non-degenerate quadrilateral in which all angles are right angles and each corner is the reflection of the opposite corner across the corresponding diagonal.
We can also talk about a square built on a line segment as simply a square one of whose sides is that line segment. Note that there are always two squares built on a given line segment, but that won't be an issue here.
Finally, we can talk about scissors congruence; this basically boils down to talking about interiors of polygons and rigid motions. Luckily, in our case we just have to talk about squares and triangles, so that simplifies the language substantially. We have to be a bit careful here since we can't quantify over finite sequences (so "$\mathcal{A}$ is scissors-congruent to $\mathcal{B}$" isn't first-order expressible) but we can talk about scissors congruences involving dissection into a fixed number of pieces, and this is enough for us since we have an explicit dissection in mind.

We can now state Pythagoras' theorem in the language of "pure geometry" (with some automatially-translatable abbreviation). In particular this avoids any reference to measurements by numbers (either of lengths or angles):

(PT) Suppose $\angle ABC$ is a right angle and $\mathcal{A,B,C}$ are squares built on line segments $\overline{BC}$, $\overline{AC}$, $\overline{AB}$ respectively. Then we can cut-and-rearrange $\mathcal{B}$ into $\mathcal{A}$ and $\mathcal{C}$.

With the statement in pure geometry in hand, it's not surprising that (PT) can be proved from some natural axiom system for pure geometry in hand. Of course that's a nontrivial task ... but it is doable, and in fact multiple of the "standard" proofs of Pythagoras' theorem translate to such more-or-less automatically.

Is Pythagoras' Theorem a theorem?

2 Answers2

Linked